최소제곱법 (Least Square Method) 정리

목차

1. Least square method

2. Revisited orthogonality principle

3. Minimum error squares sum

4. Normal equation과 Linear least-squares filters

5. Time-average correlation matrix $\Phi$

6. Data matrix를 이용한 Normal equation 재구성

7. Least-squares estimate의 property

---

※ 수식 전개는 계산 용이성을 위해, complex가 아닌 real을 가정하였습니다.

오차의 제곱합을 최소화하는 최소제곱법(Method of Least Squares)에 대해 알아봅시다. 

 

1. Least square method

	Wiener filter	Least Square Method
데이터 특성	Random (WSS random process)	Deterministic (fixed data)
최적화 기준	모든 realization에 대해 최적화	주어진 데이터에 대해 최적화
필터 설계 목표	평균제곱오차(MSE) 최소화	오차 제곱합 최소화
적용 예시	신호 복원, 오디오 잡음 제거	데이터 모델링, 회귀 분석

 

Wiener filter는 대표적인 bayesian esimator로, 관측한 데이터를 시간에 따라 변하는 확률적(random) 신호로 간주하며 모든 가능한 확률 과정의 실현(realization)에 대해 MSE를 최소화하도록 설계됩니다. Least Square Method는 대표적인 classical estimator로, 관측한  데이터가 random하지 않고 deterministic하다고 간주하며 주어진 데이터에 대해 오차 제곱합을 최소화하도록 설계됩니다.

 

* WSS (Wide Sense Stationary): 평균과 분산이 시간에 따라 변하지 않고 일정한 성질을 가짐

* Deterministic: 데이터가 특정 규칙에 따라 주어진 고정된 값을 가짐

 

 

위 다중 선형 회귀 모델에서, $e_o(i)$는 평균이 0이고 분산이 $\sigma^2$인 white noise라고 가정합니다. 선형 최소제곱 추정 문제는 주어진 입력 데이터 $u(i)$와 원하는 신호 $d(i)$를 가지고 오차 $e(i)$를 최소화하는 $w_{ok}$를 추정하는 것을 목표로 합니다.

 

 

데이터 윈도잉은 신호를 처리할 때 데이터의 경계 처리 방법을 정의합니다. 주어진 데이터는 보통 $i=1$부터 $i=N$까지 관측되지만, 실제 계산 과정에서는 데이터 경계 밖의 값 $i<1$ 또는 $i>N$을 어떻게 처리할지 가정이 필요합니다. 이 챕터에서는 다양한 데이터 윈도잉 방법 중, covariance method를 가정합니다.

 

Covariance method는 정확하게 계산 가능한 부분만 추려내어 오차(error)를 계산할 수 있다는 장점이 있습니다. 하지만, 데이터의 경계 부분에서는 원소가 덜 사용되고 가운데 원소일수록 최대 $M$번까지 사용되므로, 행렬의 양 끝단일수록 상대적으로 영향력이 작아지는 단점이 있습니다.

 

2. Revisited orthogonality principle

 

3. Minimum error squares sum

 

4. Normal equation과 Linear least-squares filters

Normal equation은 wiener filter의 wiener-hopf equation에 해당합니다.

 

 

Normal equation의 $\Phi$ 행렬은 대각 성분이 모두 다른 값을 가지기 때문에 토플리츠 행렬이 아니라는 점에서 wiener-hopf equation에서의 $\textbf{R}$ 행렬과 다릅니다. 

 

 

5. Time-average correlation matrix $\Phi$

 

6. Data matrix를 이용한 Normal equation 재구성

$\textbf{P}$는 projection operator

 

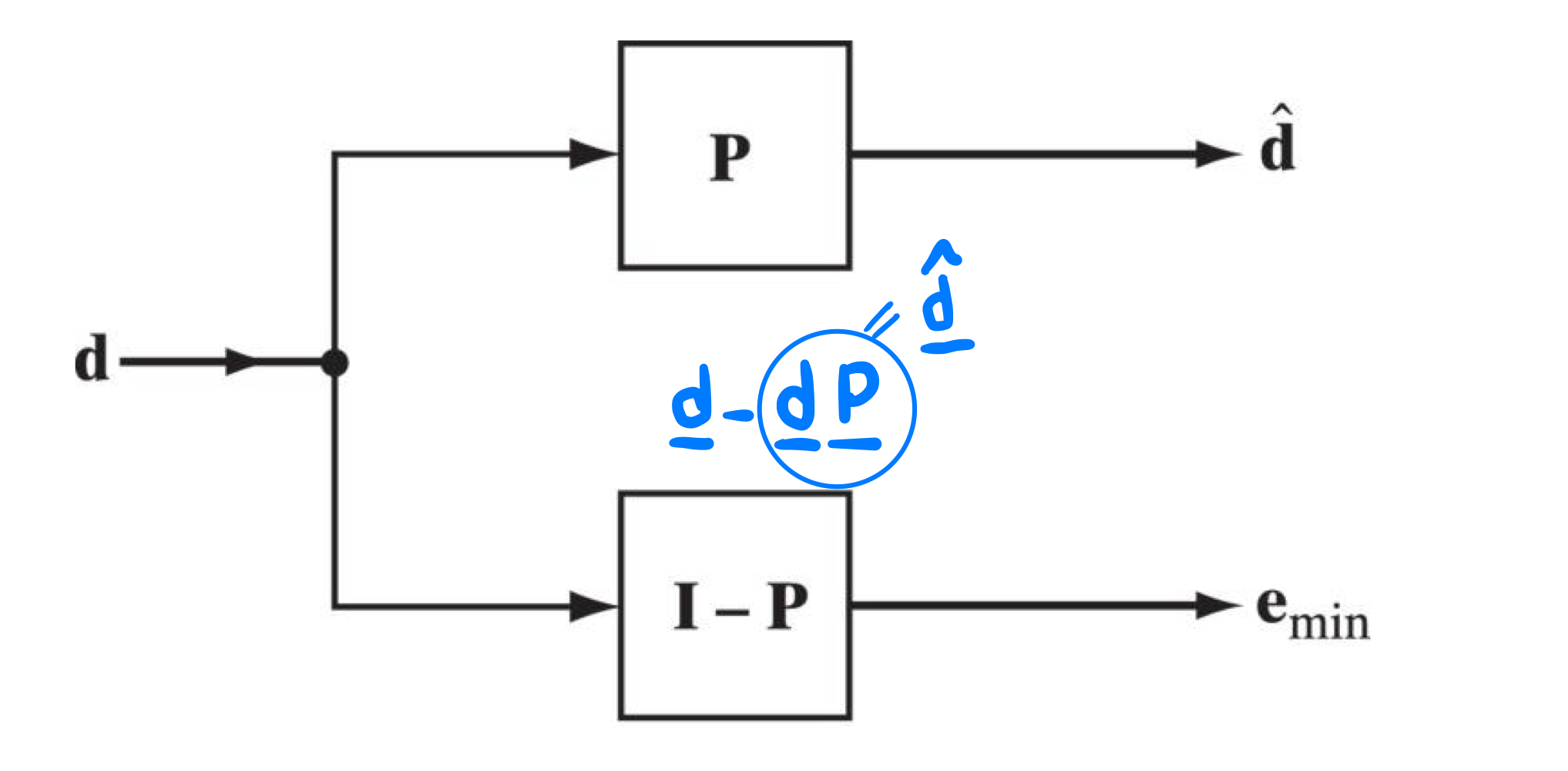
7. Least-squares estimate의 property

 

 

 

 

Wiener filter에 대한 내용을 살펴보고 싶으시다면, 아래 게시글을 참고해주세요 :)

 

Wiener filter 총정리

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.