Wiener filter 총정리

목차

1. Wiener filter

2. MMSE criterion을 만족하는 최적의 FIR filter

3. Orthogonality principle

4. Minimum mean-square error

5. Wiener-Hopf equation

6. Error-performance surface

 

---

수식 전개는 계산 용이성을 위해, complex가 아닌 real을 가정하였습니다.

1. Wiener filter

 

MMSE (minimum mean square error) 최소화하도록 설계된 최적의 linear discrete-time filter를 wiener 필터라고 합니다. 다시 말해, 필터 출력 $y(n)$이 원하는 신호 $d(n)$에 근사하도록 추정 오차 $e(n)=y(n)-d(n)$을 최소화하는 방향으로 wiener 필터가 설계된다고 이해할 수 있겠습니다.

 

Wiener 필터 설계 시, FIR로 구현할 것인지 아니면 IIR로 구현할 것인지 고민이 필요합니다. FIR 필터는 IIR에 비해 더 많은 계수를 요구하지만, 안정성이 높다는 장점이 있습니다. 필터 계수가 시간에 따라 변하는 상황에서는 안정성이 중요한데, 이때 FIR 필터가 적합합니다. 

 

추정 오차를 최소화하기 위해 쓰는 대표적인 statistical criterion으로는 MSE (mean-square error)와 MAE (mean absolute error)가 있습니다. MSE는 제곱을 하면 항상 값이 양수가 되고 미분도 비교적 간단하게 수행할 수 있기 때문에 경사하강법(gradient descent)과 같은 알고리즘 에서 많이 쓰입니다.

 

2. MMSE criterion을 만족하는 최적의 FIR filter

 

MMSE criterion을 따른다고 했을 때, 목표는 $e(n)$의 제곱 평균을 최소화하는 것입니다. 이를 위해, cost function의 미분을 0으로 만드는 필터 계수 $w_k$를 찾아 최적의 값을 구합니다.

 

3. Orthogonality principle

MMSE 최적화 문제에서 추정 오차 $e(n)$이 필터 입력 신호 $u(n)$이 생성하는 부분 공간 (subspace)에 대해 직교해야 합니다. 이를 이해하기 위해, 다음과 같이 수식을 전개하였습니다. 

 

 

MMSE criterion에서는 cost function을 최소화하는 것이 목표이기 때문에, 그 미분값은 0이 되어야 합니다.

 

$$E[u(n-k)e_o(n)]=0$$

$e_o$: optimal filter의 추정 오차

 

따라서, cost function $J$가 최소화될 때, 추정 오차 $e(n)$은 각 입력 신호에 대해 orthogonal 합니다.

 

 

Wiener 필터의 optimal한 출력 $y_o(n)$는 입력 신호 $u(n)$과 필터 계수 $w_k$의 선형 결합으로 이루어집니다. 그렇기 때문에, MMSE를 만족하는 최적의 wiener 필터에서 오차가 모든 입력 신호에 orthogonal 하면, 출력 신호 또한 모든 오차에 orthognal 합니다. 

 

4. Minimum mean-square error

 

여기서 $\hat{d}(n|{\mathcal{U}}_n)$은 필터 출력으로, ${\mathcal{U}}_n$이라는 신호를 기반으로 구한 $d(n)$의 추정치를 의미합니다. $d(n)$을 나타낸 식에 mean square를 취해주면, ${\sigma }_d^2={\sigma }_{\hat{d}}^2+J_{min}$과 같이 분산에 대한 식을 얻을 수 있습니다. 모든 항이 0보다 크거나 같다는 것을 생각해보면, 추정치의 파워가 원신호의 파워보다 작거나 같다는 걸 알 수 있습니다. 위 식의 경우, 신호 파워가 커지면 오차도 비례해서 커지기 때문에, desired signal power인 ${\sigma }_d^2$로 normalize하는 과정이 필요합니다.

 

5. Wiener-Hopf equation

 

orthogonal principle 식에서 $e(n)$을 풀어 써서 정리하면, filter input의 autocorrelation function과 filter input과 desired signal 간 cross-correlation을 하나의 관계식으로 나타낼 수 있는데 식을 Wiener-Hopf equation이라고 합니다.

 

 

위 그림에서는 $M$ tap FIR filter일 때 Wiener-Hopf equation을 matrix notation으로 표기하였습니다. 여기서 ${\mathrm{w}}_o$는 찾고자 하는 optimal filter coefficient를 의미하고 $\mathrm{R}$은 input signal의 autocorrelation matrix, $\mathrm{p}$는 input과 desired 간 cross-correlation vector를 나타냅니다.

 

6. Error-performance surface

* cost function $J$

 

$J$는 filter의 tap-weight에 대한 2차 함수입니다. Error-performance surface도 filter의 tap-weight를 기준으로 하는 error 함수에 대한 곡선으로 다차원 공간에서 bowl-shaped 2차 함수 형태로 나타납니다. tap weight 벡터는 자유도가 $M$이므로, error-performance shape는 cost function 축까지 포함하여 $(M+1)$차원으로 나타납니다. Surface는 tap-weight 변화에 따른 error 변화를 보여주는 것으로, 최저점에서 error가 최소화됩니다.

 

 

 

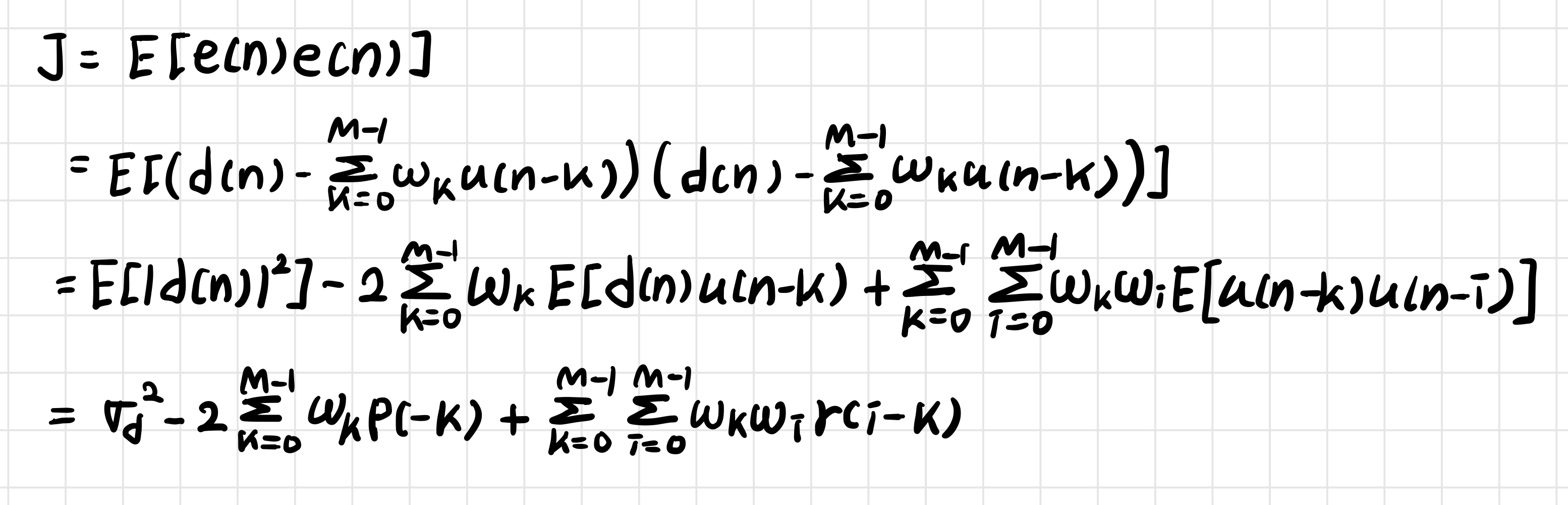
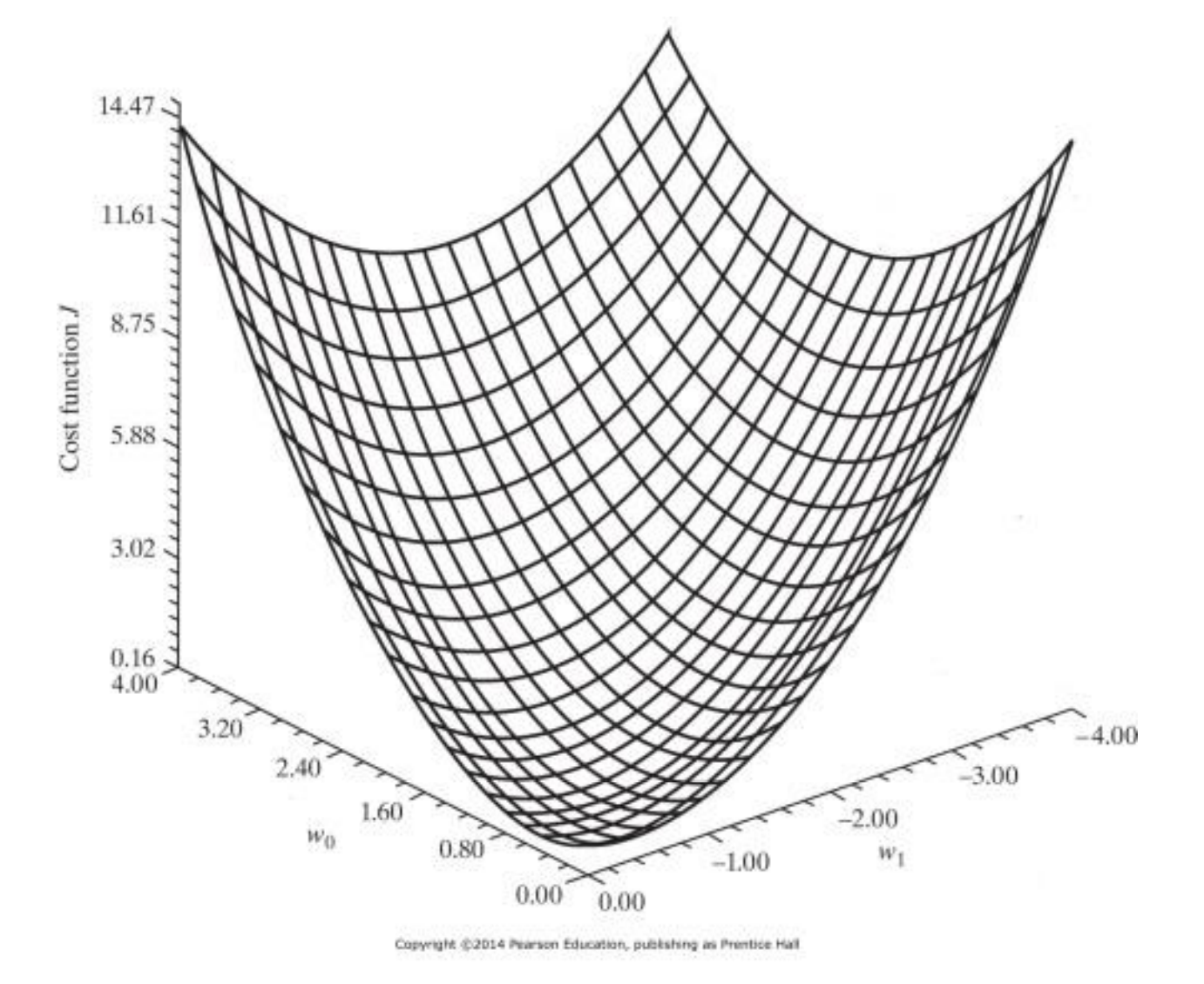
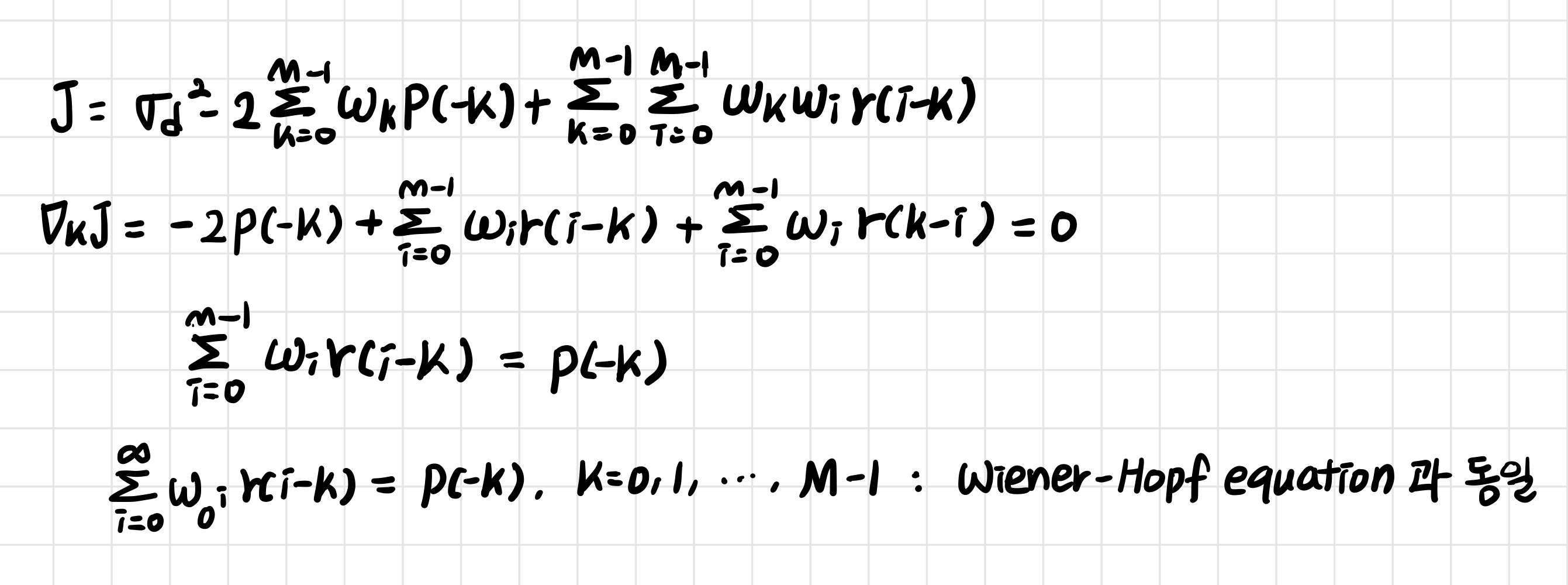
* Minimum MSE

 

 

* Error-performance surface의 canonical form

 

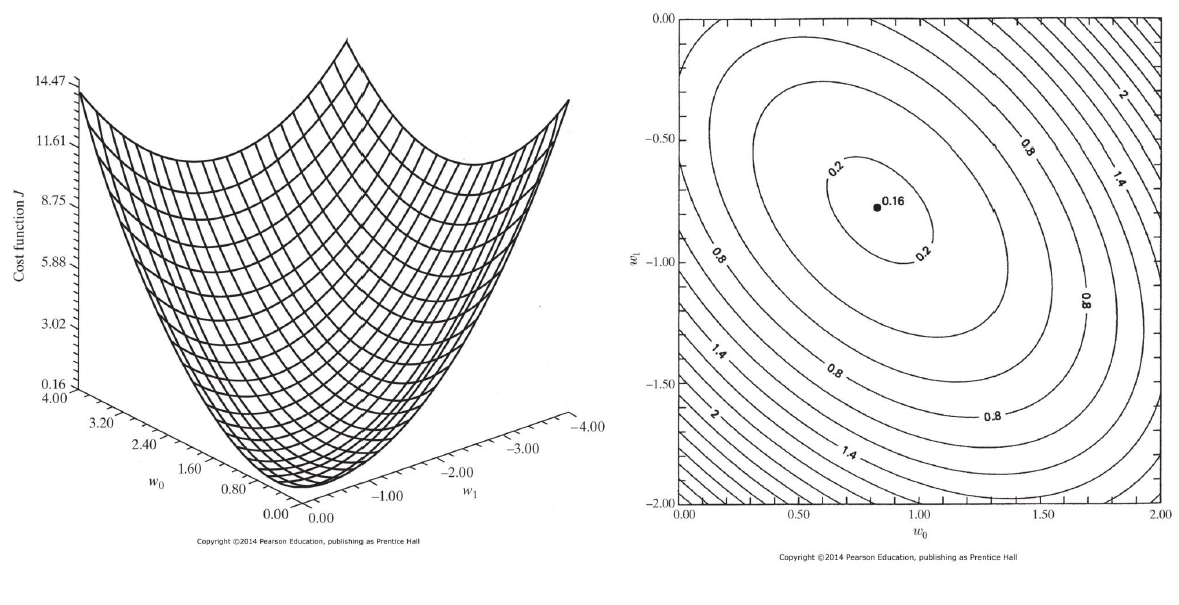
일반적으로 error-performance surface의 최저점이 optimal point가 됩니다. 이 값은 eigen decomposition을 이용해 현재 값에 상관 없이 한 번에 최적값을 구하거나 gradient descent를 이용해 현재값을 가지고 차근차근 최적값을 찾아가는 방식으로 구할 수 있습니다. 

 

 

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.