Kalman Filter 정리

목차

1. Kalman filter란 무엇인가?

2. Scalar random variable에 대한 Recursive linear MMSE estimation

3. Kalman filter 문제 정의

4. Innovation process

5. Innovation process를 이용한 state estimation

6. Filtering

7. Kalman filter 요약 정리

8. RLS filter의 통합적 기반으로서의 Kalman filter

---

※ 수식 전개는 계산 용이성을 위해, complex가 아닌 real을 가정하였습니다.

 

1. Kalman filter란 무엇인가?

Kalman filter는 Wiener filter를 확장한 것으로, state space 개념을 도입한 필터입니다. 현재 state에서 다음 state를 결정하는 process equation과 current state를 기반으로 observation vector를 결정하는 measurement equation로 구성되어 있습니다. 해(solution)는 재귀적으로 계산되며, Kalman filter는 일반적으로 최적의 linear MMSE estimator로 작동합니다. 그리고, jointly Gaussian인 경우에는 최적 MMSE estimator가 됩니다. 또한, Kalman filter는 RLS filter를 위한 통합 프레임워크(unifying framework)를 제공합니다. 

 

2. Scalar random variable에 대한 Recursive linear MMSE estimation

 

위의 observed random variable과 observation을 기반으로 $x(n-1)$을 추정한 linear MMSE estimator가 있다고 가정해봅시다. innovation $\alpha (n)$은 새로운 observation $y(n)$에서 과거 정보 $y(n-1)$로부터 예측할 수 있는 부분을 제외한 나머지, 즉 예측 불가능한 부분이자 새로운 정보에 대한 측정값입니다. innovation $\alpha (k)$가 $x(n)$을 추정하는데 얼마나 기여하는지 나타내는 가중치는 $b_k$로 정의되는데 이 값은 $\alpha (k)$ 와 추정 대상인 $x(n)$ 간의 상관관계에 따라 결정됩니다. 

 

 

위 그림은 linear MMSE estimation의 재귀적 과정을 시각화한 것입니다. Time udpate에서는 현재 시점 $n-1$에서 다음 시점 $n$의 observation $y(n)$을 예측하기 위해, 이미 가지고 있던 state 추정값을 기반으로 예측값 $\hat{y}(n|\mathcal{Y}_{n-1})$을 구합니다. Measurement update에서는 새로운 관측값 $y(n)$이 도착하면 이를 바탕으로 기존 state 추정값 $\hat{x}(n-1|\mathcal{Y}_{n-1})$에 innovation tem인 $b_n \alpha (n)$을 추가해 새로운 추정값 $\hat{x}(n|\mathcal{Y}_{n})$을 계산합니다.

 

3. Kalman filter 문제 정의

 

위 그림은 Kalman filter의 수학적 모델을 system equation과 measurement equation을 통해 설명하고 state 예측과 observation을 시각화한 것입니다. 이 시스템은 시간에 따라 변화하며, observation은 시스템의 state에 노이즈가 섞여 반영됩니다. 이 시스템의 state를 재귀적으로 추정하는 것이 Kalman filtering 문제의 핵심입니다. 여기서 $\textbf{x}(n)$은 $M$차원 state vector로, 시스템의 미래 행동을 예측하는데 필요한 과거 행동에 대한 최소한의 데이터 집합을 나타냅니다. $\textbf{y}(n)$은 $N$차원 observation vector 입니다. 

 

 

4. Innovation process

 

앞에서 보았던 innovation process의 성질 3가지를 통해, 시스템의 dynamic model에서 각 time step에서의 state와 noise 간 상호 독립성을 확인할 수 있습니다. 

 

 

5. Innovation process를 이용한 state estimation

 

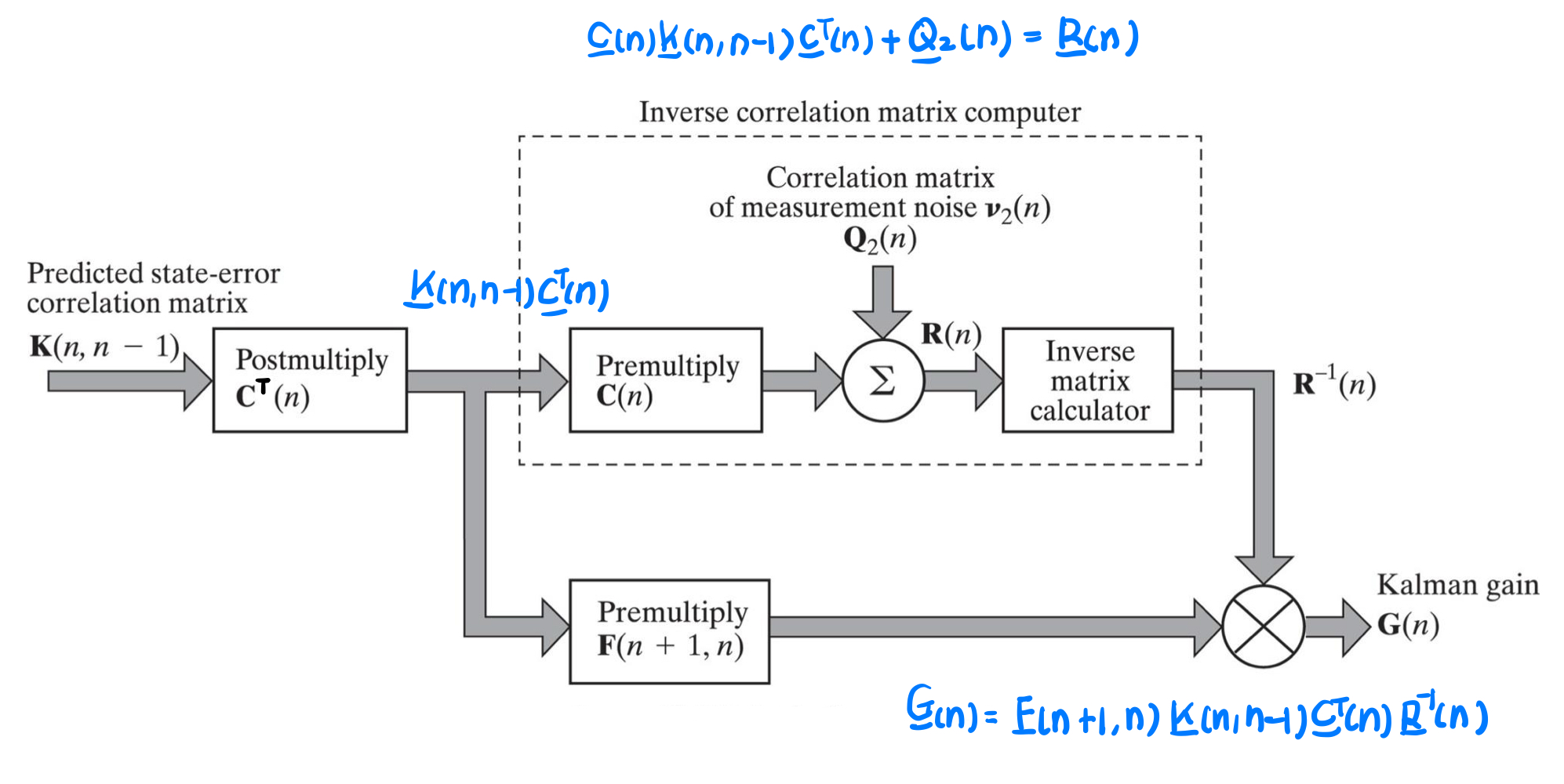
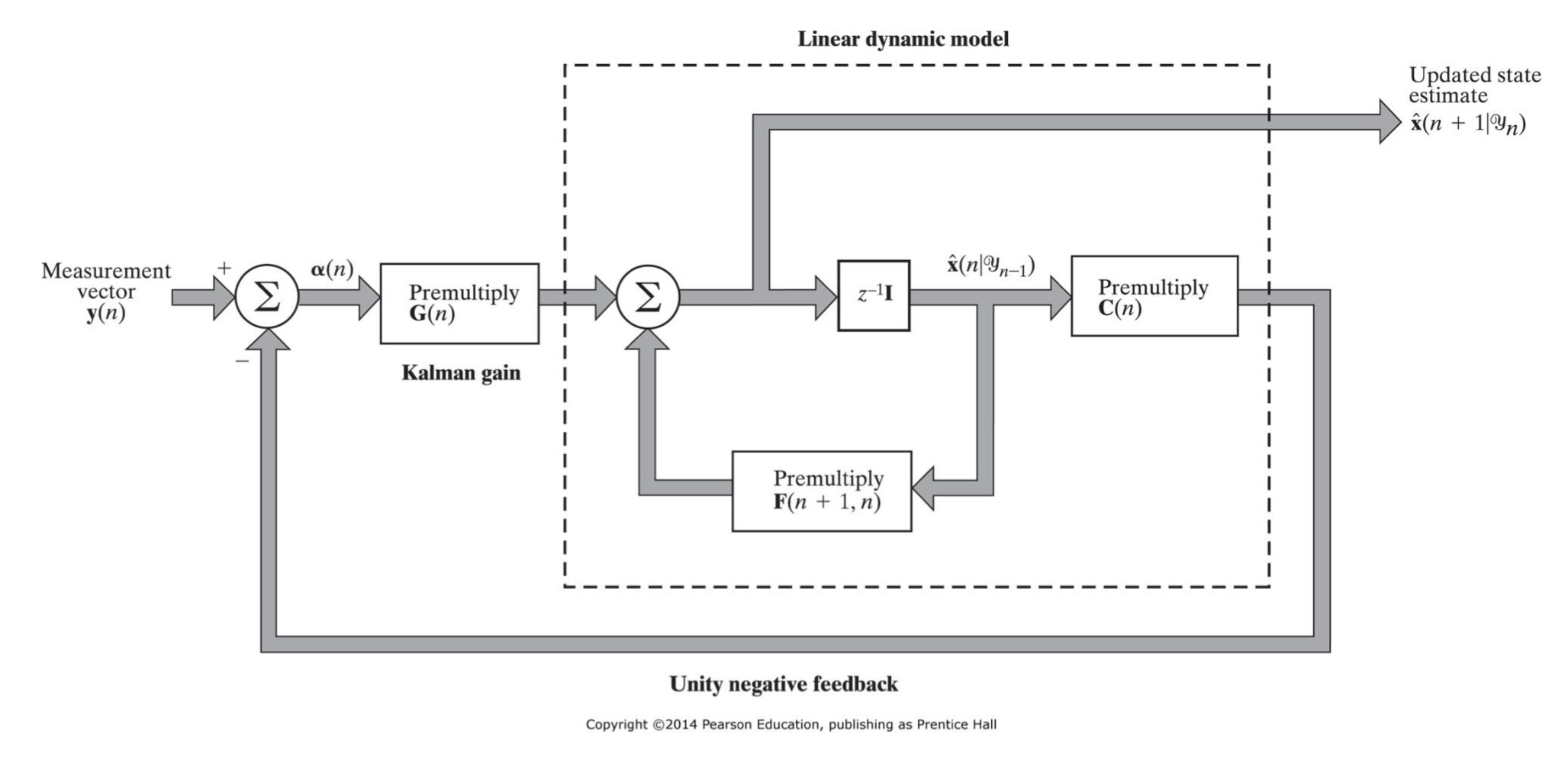
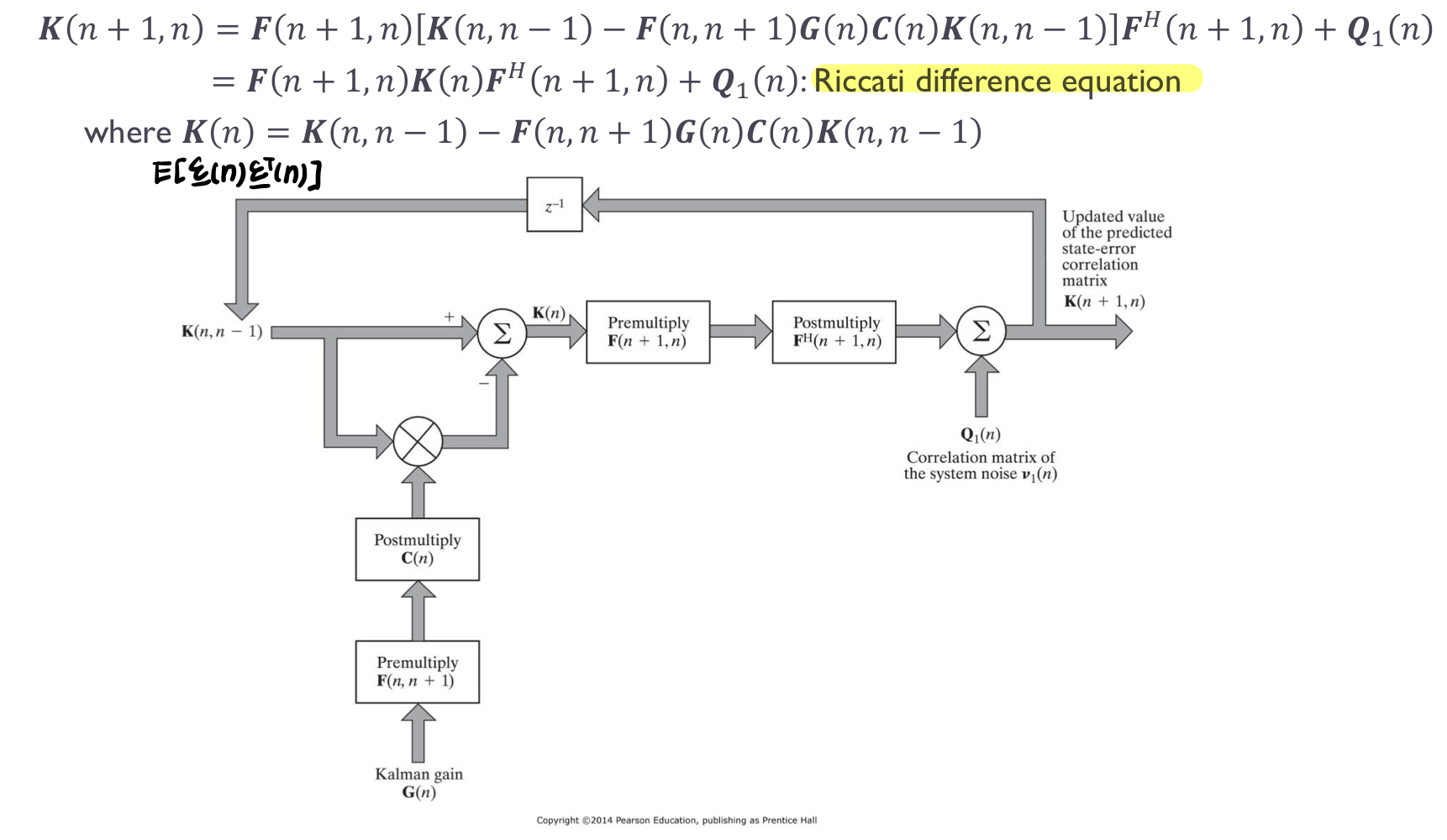
6. Filtering

 

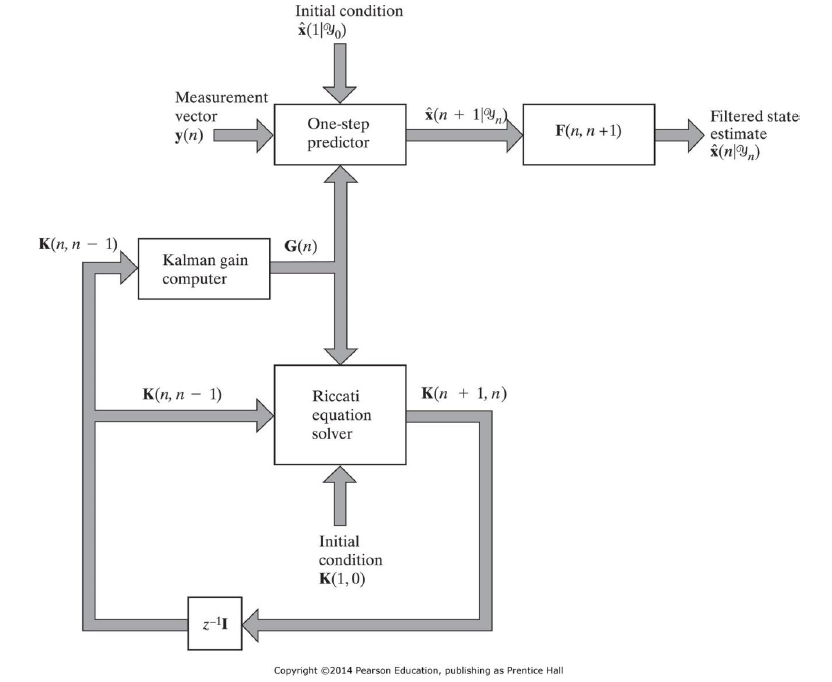
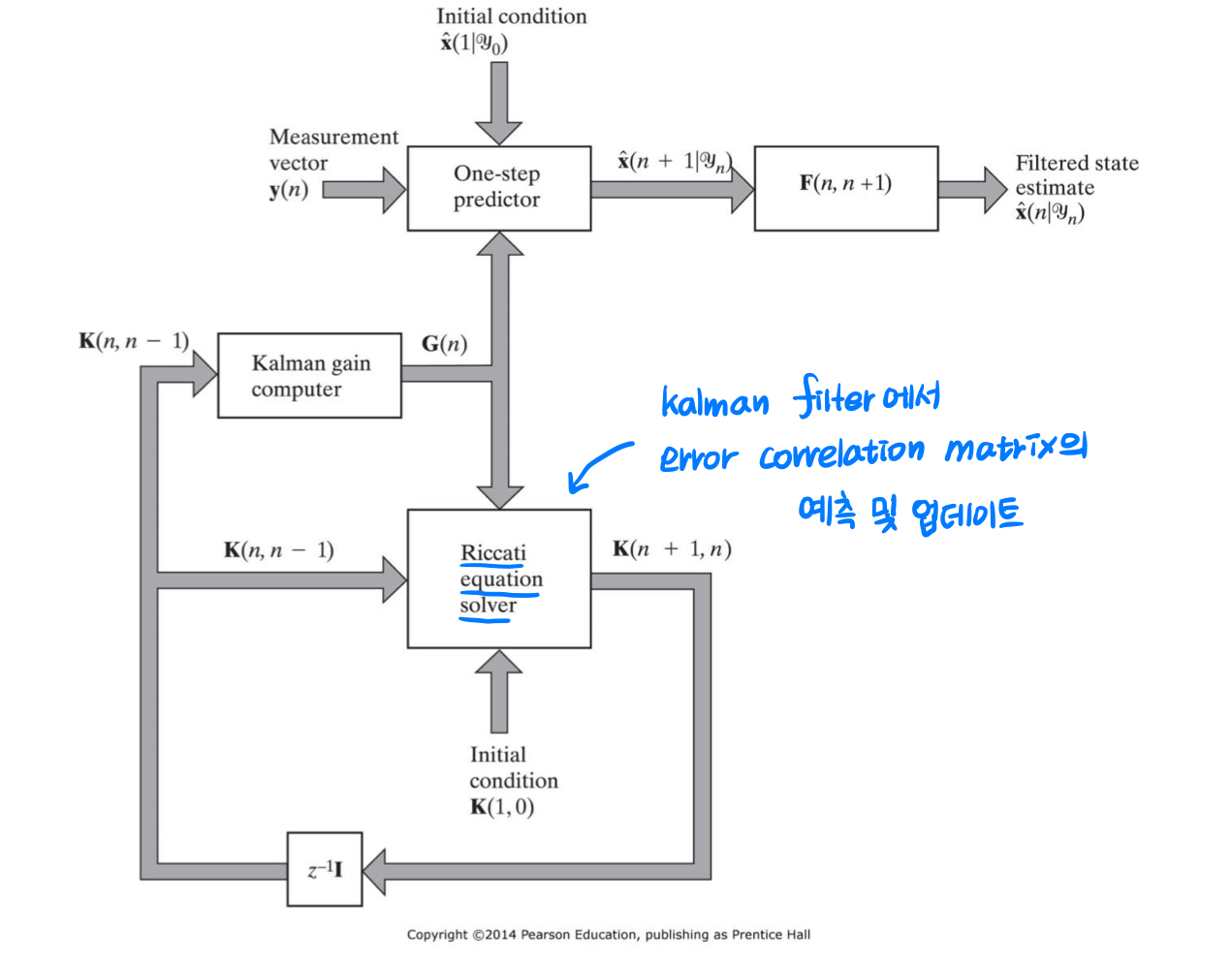
7. Kalman filter 요약 정리

 

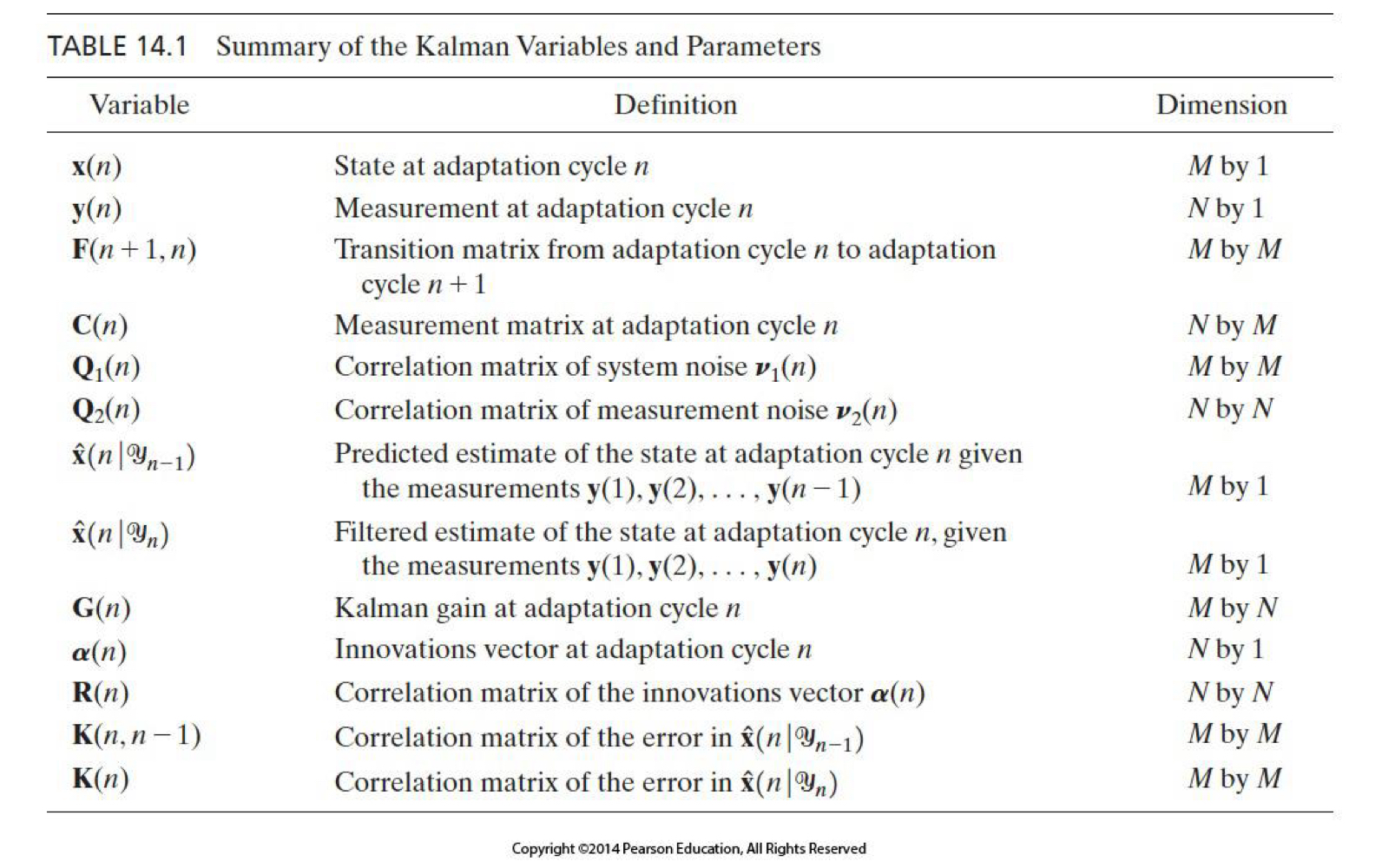
위 그림은 Kalman filter의 구성 요소와 계산 절차를 요약한 것입니다. Kalman Gain과 Innovation process, state 업데이트를 업데이트하고 error correlation matrix를 최소화하는 방식으로 동작함으로써, 필터가 최적의 state를 추정을 수행하는 과정을 보여줍니다.

 

 

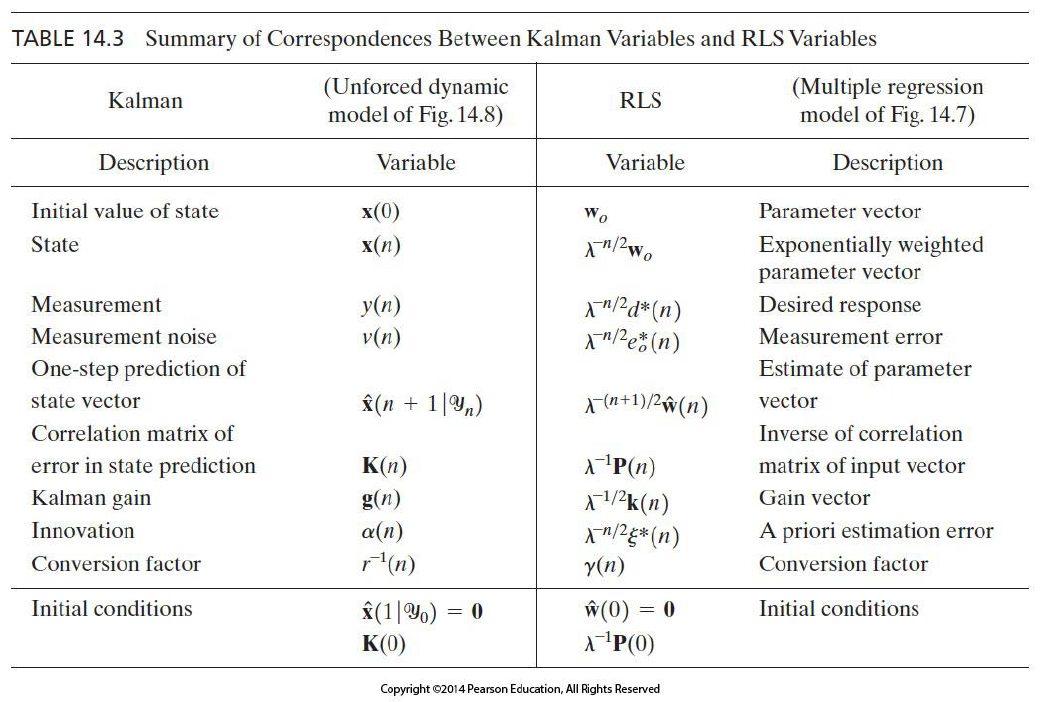
8. RLS filter의 통합적 기반으로서의 Kalman filter

 

Kalman filter는 state space 모델을 기반으로 동작하며, 시간에 따른 state를 추정합니다. RLS filter는 가중치를 업데이트하여 prediction error를 최소화합니다. Kalman filter의 state $\hat{\textbf{x}}(n+1|\mathcal{Y}_n)$를 RLS filter의 가중치와 연결하는 변환행렬 $\varphi (n)\hat{\textbf{w}}(n)$로 바꾼 위 수식 전개를 통해, Kalman filter와 RLS filter는 동일한 수학적 구조를 가지며 변환 및 스케일링을 통해 두 필터가 동일한 문제를 서로 다른 방식으로 해결한다는 점을 확인할 수 있습니다.

 

 

Kalman filter와 RLS filter가 시간에 따라 exponential하게 감소하는 동일한 스케일링 패턴을 따라 state vector와 출력값이 위와 같이 정의되는 것을 알 수 있습니다.

 

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.