Recursive Least-Square (RLS) Adaptive Filter 정리

목차

1. Recursive least squares adaptive filters

    1-1. RLS 알고리즘이란 무엇인가?

    1-2. Regularization

    1-3. Normal equation Reformulation

    1-4. $\mathbf{\Phi }(n)$와 $\mathbf{\text{z}}(n)$의 재귀적 연산 (Matrix inversion lemma 사용)

    1-5. Tap-weight vector의 time update

    1-6. RLS 알고리즘 한 눈에 보기

2. RLS algorithm의 convergence analysis

    2-1. Assumption

    2-2. Mean value에서 RLS 알고리즘의 수렴

    2-3. RLS 알고리즘의 mean-square deviation

    2-4. RLS 알고리즘의 Ensemble-average learning curve

---

※ 수식 전개는 계산 용이성을 위해, complex가 아닌 real을 가정하였습니다.

최소제곱(Least Squares)을 재귀적으로 업데이트하는 RLS (Recursive Least-Square) 알고리즘을 정리해봅시다.

 

1. Recursive least squares adaptive filters

1-1. RLS 알고리즘이란 무엇인가?

RLS 알고리즘은 이전 시간 스텝 $n-1$에서 계산된 필터 탭 가중치 벡터의 최소제곱 추정치를 기반으로, 새로운 데이터가 입력되면 현재 시간 스텝 $n$에서 업데이트된 추정치를 계산합니다. 데이터의 inverse correlation matrix를 사용하여 입력 데이터를 whitening하기 때문에 LMS (Least Mean Square) 알고리즘보다 수렴 속도가 더 빠릅니다. 

 

 

RLS 알고리즘은 위 cost function $\epsilon (n)$을 최소화하며 가중치 계수로 $\beta (n,i)$를 사용합니다. $\beta (n,i)$ 은 nonstationary 환경에서도 adaptive하게 동작할 수 있도록 최근 데이터에 더 많은 가중치를 부여합니다.  

 

 

1-2. Regularization

Least-squares 추정은 ill-posed inverse problem이라는 특성 때문에 아래와 같은 문제를 가집니다.

 

1. 입력 데이터만으로 입력-출력 간 관계(mapping)를 고유(unique)하게 복원하기엔 정보가 부족합니다.
2. 입력 데이터에 노이즈가 포함되어있거나 값이 부정확하면 입력-출력 간 관계를 정확하게 파악하기 어려워집니다(uncertainty).

Least-squares 추정을 well-posed problem으로 만들기 위해서는, 사전 정보(prior information)을 cost function에 포함시킬 필요가 있습니다. 다시 말해, 입력 데이터만으로는 불충분하거나 불확실성이 클 수 있기 때문에, 추가적인 제약이나 규제를 cost function에 반영하여 문제를 명확하게 해결할 수 있도록 해야 합니다. 

 

 

1-3. Normal equation Reformulation

 

1-4. $\mathbf{\Phi }(n)$와 $\mathbf{\text{z}}(n)$의 재귀적 연산 (Matrix inversion lemma 사용)

 

1-5. Tap-weight vector의 time update

 

1-6. RLS 알고리즘 한 눈에 보기

 

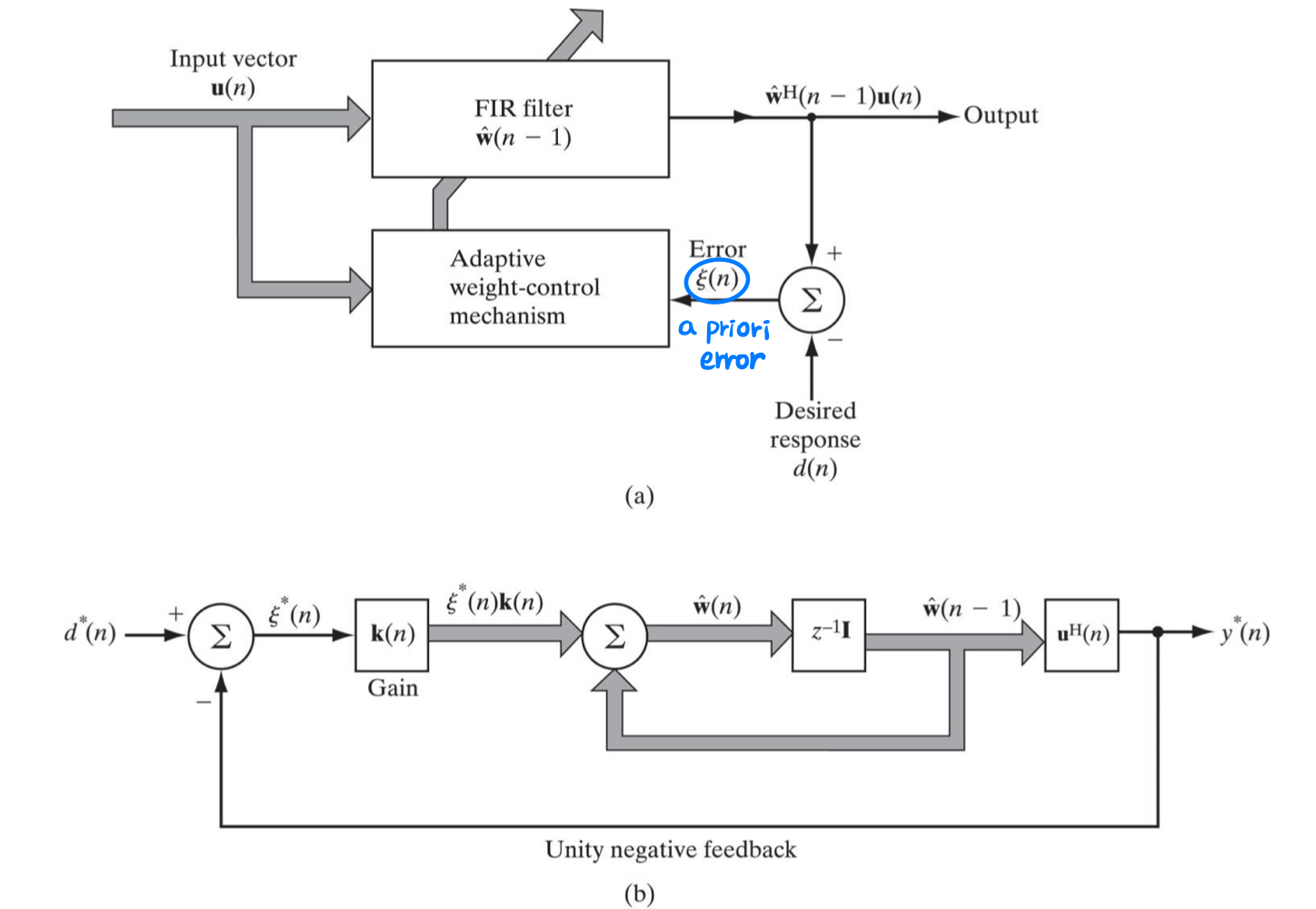
2. RLS algorithm의 convergence analysis

2-1. Assumption

 

[용어정리]

• stochastic process: 확률적인 규칙에 따라 데이터가 생성됨
• ergodic: 시간에 따른 평균이 확률적인 평균과 같음, 샘플 데이터가 전체 확률 분포를 잘 대표함

 

2-2. Mean value에서 RLS 알고리즘의 수렴

 

2-3. RLS 알고리즘의 mean-square deviation

 

2-4. RLS 알고리즘의 Ensemble-average learning curve

 

 

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.