Fast block LMS 알고리즘 이해하기

목차

1. Block adaptive filter

2. Fast block LMS algorithm

 

---

1. Block adaptive filter

 

Block adaptive filter는 $L$개의 샘플 데이터로 이루어진 블록마다 filter weight를 업데이트하며, 각 블록에 동일한 filter weight가 적용됩니다. LMS filter가 매번 단일 데이터 값만을 사용해 weight를 업데이트하는 것과 달리, Block adaptive filter는 최근 $L$개의 데이터 값을 이용해 time average를 구하고 이를 바탕으로 weight를 계산합니다. 수렴 속도와 MSE 최솟값은 LMS와 거의 동일합니다.

 

2. Fast block LMS algorithm

 

Fast block-LMS 알고리즘은 주파수 영역에서 FFT를 사용하여 구현됩니다. convolution 식 $y(n)= h(n)*u(n)$에서 필터 $h(n)$과 신호 $u(n)$의 길이가 각각 $M$과 $L$일 때, linear convolution 결과는 $L+M-1$개의 nonzero 값들을 가지게 됩니다. 필터의 DFT 계수와 신호의 곱은 circular convolution 결과로 나오게 되는데, 이로 인한 artifact를 없애고 linear convolution과 같은 결과를 출력하게 만들기 위해, 전체 길이를 나타내는 $N$이 $L+M-1$보다 크거나 같도록 만들어줍니다. 이러한 이유로, $h(n)$과 $u(n)$에 zero-padding을 적용하여 FFT를 수행합니다. 만약 신호 $u(n)$이 무한한 길이를 가지고 이를 블록 단위 convolution으로 계산하고자 한다면, $L$ 길이의 $u(n)$에서 $L$길이의 $y(n)$을 계산해야 합니다. 이를 구하기 위해, 주로 사용되는 방법으로는 Overlap-add와 Overlap-save 방식이 있습니다. 

 

* Overlap-add method

아주 긴 신호가 입력으로 들어왔을 때, 이 신호를 $L$개 샘플 데이터로 이루어진 segment로 자릅니다. 이렇게 분할한 $L$ 길이의 입력 데이터로부터 $IFFT_N[FFT_N(h(n)) \cdot FFT_N(u(n))]$을 계산하고, $L + M - 1$ (DFT point $N$이 충분히 길기 때문에 artifact 발생 X)길이의 출력을 얻습니다. $M - 1$ 길이의 겹치는 출력은 다음 프레임에 더해가는 방식으로 동작합니다. 

 

* Overlap-save method

Overlap-save method는 각 블록에서 생긴 circular convolution artifact를 잘라버리고 안전한 부분만 쓰는 방법입니다. 안전한 부분이 $L$개가 되어야 하므로 입력의 길이는 $L+M-1$ 입니다.  입력 데이터 $u(n)$을 사용하여 $IFFT_N[FFT_N(h(n)) \cdot FFT_N(u(n))]$을 계산한 후, circular convolution artifact (linear convolution과 일치하지 않는 출력)가 생긴 부분을 버리고 $M$번째부터 $L + M - 1$번째까지의 출력만 사용합니다. 

 

Overlap-save method를 좀 더 자세히 알아보도록 하겠습니다. 살펴보기에 앞서, DFT와 circular convolution에 대한 사전지식이 필요합니다. 아래 링크에서 관련 내용을 참고해주세요 :)

 

DFT (Discrete Fourier Transform) 바로 알기

선형 컨볼루션 (Linear convolution)과 원형 컨볼루션 (Circular convolution)

 

DTFT의 결과는 주파수 축에서 연속적이기 때문에 컴퓨터가 직접 처리하기 어렵습니다. 따라서 디지털 신호를 처리하기 위해 연속적으로 존재하는 주파수를 쪼개서 이산적인 값으로 만드는 DFT를 사용합니다. 다시 말해, DFT는 DTFT를 주파수 영역에서 샘플링한 것으로, 이 과정에서 시간 영역에서는 aliasing이 발생하고, 이는 circular convolution으로 나타납니다. (뒤집힌 후 겹쳐져서 들어옴) 

 

 

만약 $h(n)$이나 $u(n)$ 뒤에 0이 많이 포함되어 있다면, circular convolution과 linear convolution의 결과는 동일해집니다. 그러나 신호가 짧아 0이 충분하지 않을 경우 일부 값들이 linear convolution과 달라져 문제가 발생할 수 있습니다. 이 차이를 없애기 위해서는 DFT의 길이 $N$을 충분히 길게 설정하면 됩니다. DFT 길이가 $L+M−1$ 이상이 되면, 겹치는 부분들이 0과 겹쳐져 사라지기 때문에 circular convolution artifact가 없어집니다. 즉, circular convolution artifact를 없애려면 신호 뒤에 충분한 0을 추가해주면 됩니다. 

 

$h(m)$은 $M$개의 nonzero 값을, $u_k(n)$은 $L+M−1$개의 nonzero 값을 가집니다. 여기서 $L \neq 0$이라는 가정 하에 두 신호가 겹치지 않도록 하기 위한 조건은 $M - 1 \leq n - kL < L + M - 1$입니다. 이 범위 내에서는 모든 값이 0이 되므로 circular artifact가 발생하지 않습니다. 그러나 이 범위를 벗어나면 0이 아닌 값들이 나타나면서 circular artifact가 발생하고, 이는 linear convolution과의 결과 차이를 의미합니다.

 

 

Fast block LMS 알고리즘은 주파수 영역에서 신호처리를 위해 FFT를 사용하여 필터를 적용하고 Overlap-save method를 통해 circular convolution artifact를 제거한 후 filter weight을 업데이트합니다. 

입력 신호의 길이 $L$과 필터 길이 $M$이 같고 전체길이 $N$과 $2M$이 같다는 가정 하에, 수식을 전개하였습니다. 먼저 $k$번째 블록에서 weight vector를 FFT를 통해 주파수 영역으로 변환합니다. $\textbf{U}(k)$는 diagonal matrix로, $k$번째 블록에서의 DFT 계수를 값으로 가지는 행렬입니다. Overlap-save method를 이용해 마지막 $M=L$ 개의 값만 뽑아서 출력 $\textbf{y}^T(k)$를 구합니다. 

Block LMS 알고리즘과 마찬가지로 weight를 업데이트하지만, fast block LMS 알고리즘에선 circular convolution artifact를 제거하기 위해 $\textbf{y}(k)$의 첫 $M$개의 요소를 생략하고자, 블록 error의 DFT를 구합니다. linear correlation이 linear convolution의 time reversal이라는 특성을 활용하여, 첫 번째 $M$개를 추출하고 두 번째 $M$개를 버려 $\mathbf{\phi}(k)$를 얻은 후 weight를 업데이트합니다. 

 

Fast block LMS algorithm

 

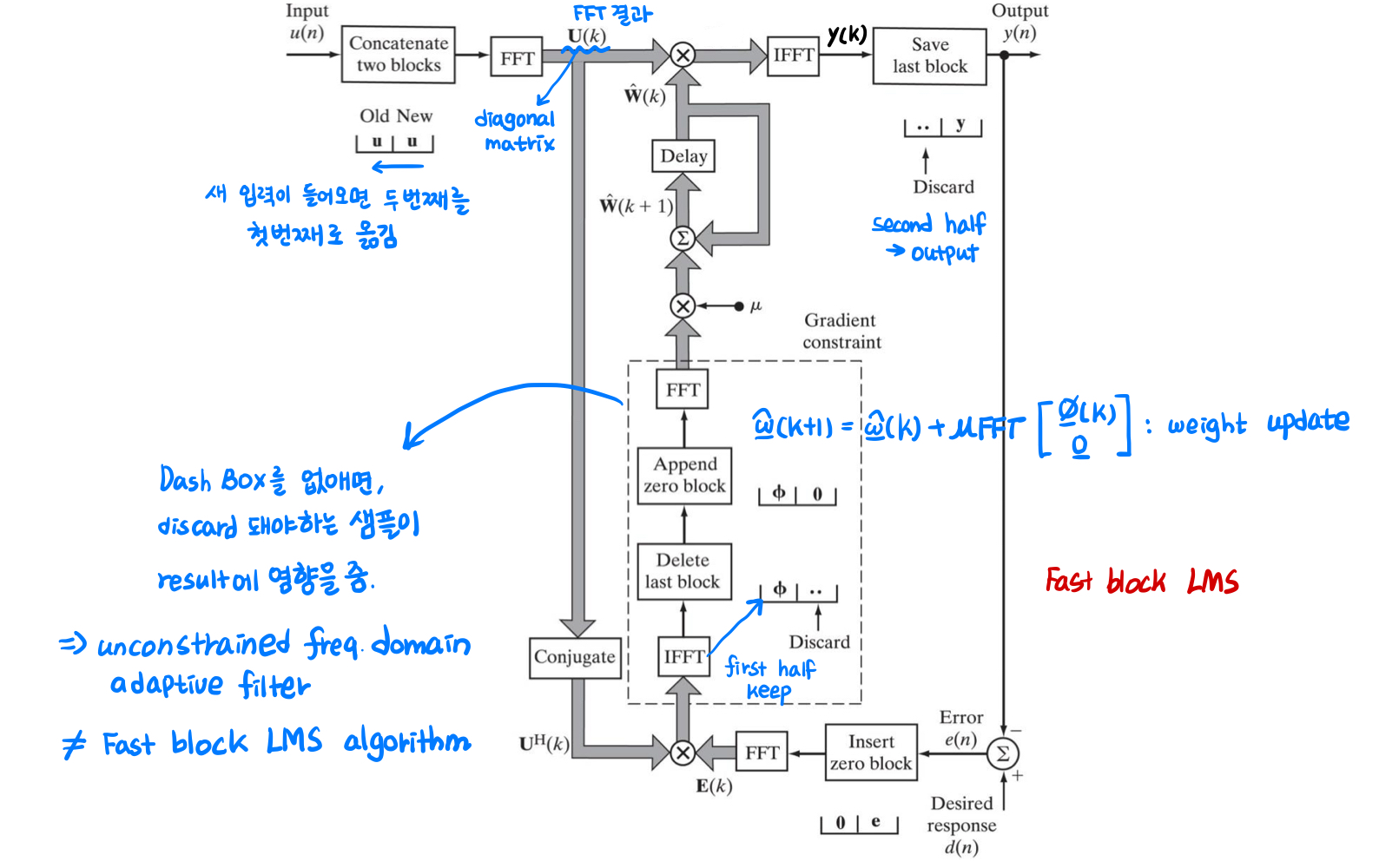
Fast block LMS 알고리즘에서 'fast'는 FFT의 빠른 계산을 의미하며, 수렴 특성 자체는 block LMS 알고리즘과 동일합니다. 그러나 Fast block 알고리즘의 수렴 속도는 각 주파수에 다른 step size, $\mu$, 를 할당하여 개선할 수 있습니다. 이 방법은 주파수별로 recursive averaging을 사용해 $k$번째 DFT 계수의 파워로 normalize해주는 방식으로 이루어집니다.

Unconstrained frequency-domain adaptive filter는 fast block LMS 알고리즘에서 보았던 dash box를 없앤 것이라고 이해할 수 있습니다. circular convolution artifact를 0으로 깔아 제거해주었던 과정을 생략한 것으로, 이로 인해 간단하고 계산량도 줄어들지만 기존의 fast block LMS 알고리즘과는 다른 결과를 얻게 됩니다. 

 

 

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.