Frequency-Domain & Subband Adaptive filter 정리

목차

1. Self-orthogonalizing adaptive filter

2. DCT-LMS algorithm

3. Subband adaptive filter

 

---

1. Self-orthogonalizing adaptive filter

 

DFT는 bandpass filter를 활용한 subband processing의 특수한 경우로 볼 수 있습니다. 따라서 filter bank나 prototype filter를 잘 설계하면 성능이 향상됩니다. 하지만 bandpass filtering 단계가 추가로 필요하고 설계가 복잡하다는 단점이 있습니다. 이를 보완하기 위해, low band과 high band를 반씩 나눠 처리하는 QMF(Quadrature Mirror Filter)를 많이 사용한다고 합니다.

Self-orthogonalizing adaptive filter는 두 단계로 구현되며, 여기서 orthogonalizing은 whitening과 동일하게 각 성분을 uncorrelated하게 만든다는 의미입니다. 즉, 입력 신호를 whitening한 후 LMS 알고리즘을 적용하는 방식으로 동작합니다. LMS 알고리즘과의 차이점은 학습률 $\mu$ 대신 $\alpha {\mathbf{\text{R}}}^{-1}$이 사용된다는 점입니다. 또한, 수식에 ${\sigma }^2$가 분모에 들어가므로 NLMS 알고리즘의 일종으로 볼 수 있습니다.

 

 

Self-orthogonalizing adaptive filter는 $\mathbf{\text{u}}(n)$을 KLT (Karhunen-Loeve transform)로 whitening한 후 LMS 알고리즘을 적용하는 두 단계로 구현됩니다. 이 과정에서 ${\mathbf{\text{R}}}^{-1}$ 을 계산해야 하므로, KLT matrix와 eigenvalue ${\lambda }_i$를 구하기 위한 eigendecomposition 과정을 거쳐야 합니다. 하지만, 실제 상황에서는 신호가 들어올 때마다 $\mathbf{\text{R}}$을 계속 업데이트하고 KLT를 다시 계산하는 것이 계산량이 많아 비효율적이기 때문에, 이를 해결하고자 KLT를 근사하는 DCT (Discrete cosine transform)를 사용하여 계산을 단순화합니다.

 

2. DCT-LMS algorithm

 

DCT는 DFT에서 real part만 취한 것이고, imaginery part만 취하면 DST (Discrete sine transform)가 됩니다. DCT-LMS 알고리즘은 sliding window에서 DCT 계수를 구한 뒤, 각 계수의 파워 (${\lambda }_i$)로 normalize하여 LMS 알고리즘을 적용합니다. 여기서 DCT를 KLT로 대체하면 self-orthogonalizing adaptive filter가 됩니다.

 

 

DCT-LMS 알고리즘에 대해 좀 더 자세히 살펴보겠습니다. $\mathbf{\text{R}}(n)$은 $\mathbf{\text{u}}{\mathbf{\text{u}}}^T$의 time average으로 정의되고 DCT matrix $\mathbf{\text{D}}$가 ${\mathbf{\text{Q}}}^H$에 근사한다고 가정하면, eigenvalue $\lambda$를 다 모아놓은 diagonal matrix $\mathrm{\Lambda }$를 구할 수 있습니다. 이 값을 이용해, sliding window 방식을 사용하여 과거의 추정치와 현재 값의 오차를 기반으로 과거 추정치를 보정하여 현재 값을 업데이트할 수 있습니다. 신호가 시간에 따라 변할 경우, 과거 정보를 덜 반영하기 위해, forgetting factor $\gamma$를 도입하여 과거 추정값을 attenuation 할 수 있습니다. 

 

3. Subband adaptive filter

 

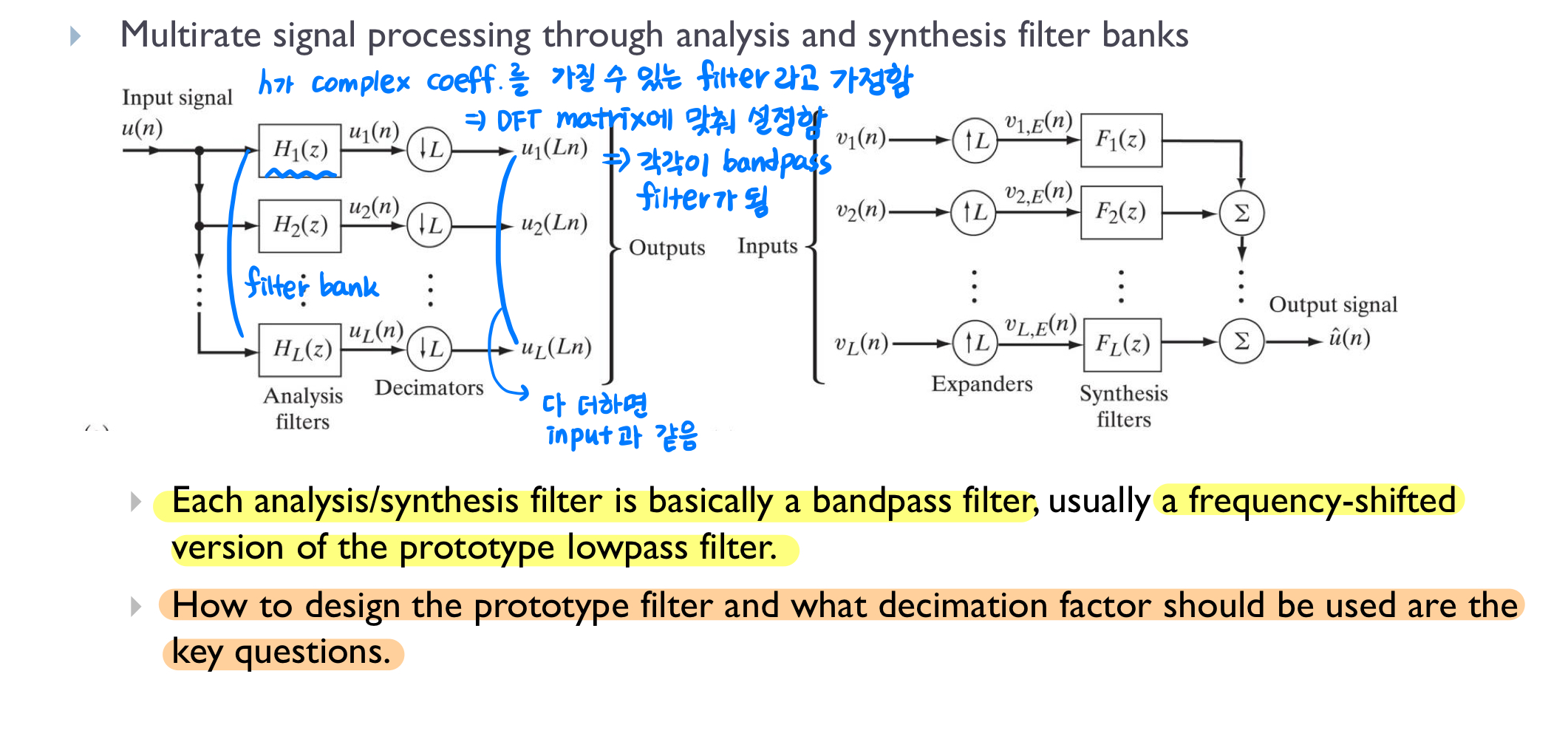
Frequency domain processing은 각 주파수 성분을 개별적으로 처리할 수 있어 time domain processing에 비해 유리한 점이 있습니다. Subband adaptive filter는 $L$개의 filter bank가 주어지면 $0$부터 $\pi$까지의 주파수 대역을 $L$개로 나눕니다. 만약 $L=2$라면, 주파수 대역은 $0$~$\frac{\pi }{2}$, $\frac{\pi }{2}$~$\pi$으로 분할됩니다. $h(n)$을 complex coefficient를 가질 수 있는 filter라고 가정하면, DFT matrix에 맞춰 $H(z)$를 설정할 수 있고, $L$개의 각각의 $H(z)$는 bandpass filter처럼 동작하게 됩니다. 하지만 $H(z)$를 단순히 bandpass filter로 보면 그다지 성능이 좋지 않기 때문에, prototype filter를 주파수 축으로 이동킴으로써 효율적인 신호 처리가 가능하도록 만들어줍니다. 그렇기 때문에, $H(z)$가 원하는 property를 갖도록 prototype filter를 잘 설계하고 적절한 decimation factor를 설정하는 게 중요합니다.

 

 

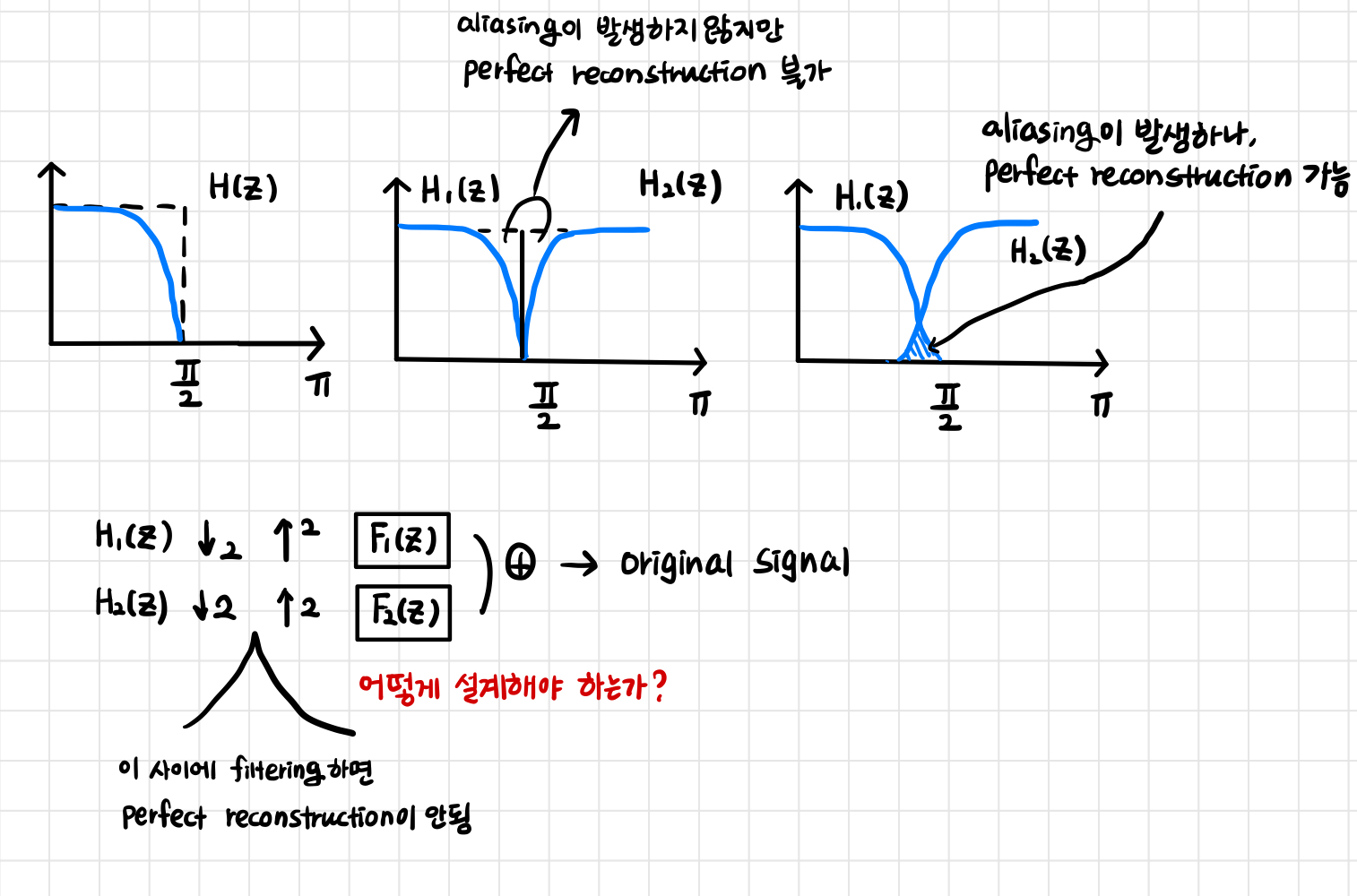
Subband adaptive filter에서 decimation factor는 각 low band signal을 얼마나 downsampling할지를 결정합니다. 다운샘플링을 통해 계산량을 줄일 수 있지만, decimation factor가 너무 크면 대역 간 에일리어싱이 발생할 수 있으므로 적절한 설정이 필요합니다.

 

다운샘플링 (Downsampling)

 

 

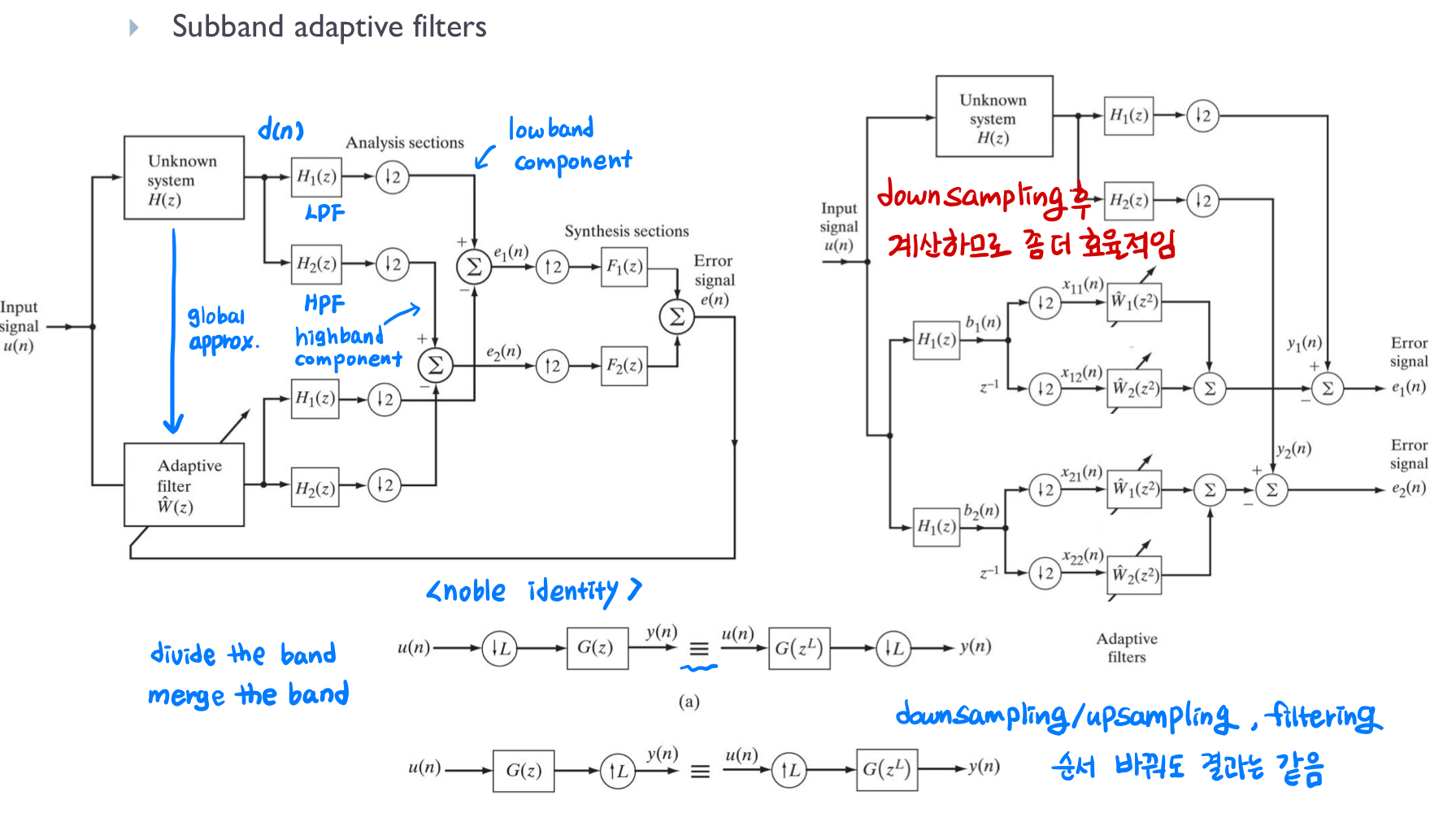
왼쪽 그림은 low band, high band로 분할한 후 따로 error를 계산하여 합산합니다. 오른쪽 그림은 홀수 번째, 짝수 번째 샘플들을 개별적으로 처리한 후 decimation을 수행하고 있습니다. 이 과정에서  noble identity를 활용하여 decimation과 filtering 연산의 순서를 바꾸면 계산량을 줄일 수 있습니다. noble identity를 적용하지 않은 방식에서는, decimation 전의 모든 샘플에 대해 필터링을 수행하므로 0인 계수와도 계속 곱셈을 해야 해서 convolution 연산이 비효율적입니다. 하지만 noble identity를 이용해 downsampling하고 filtering하면 처리해야 할 샘플 수가 줄어들기 때문에 효율적인 연산이 가능합니다. 

 

결과적으론 두 그림 모두 똑같은 결과를 출력하지만 오른쪽은 fast Block LMS 알고리즘처럼 learning rate을 서로 다른 band에서 다르게 줄 수 있고 주파수 대역별로 따로 adaptation을 시켜줄 수 있기에 time domain보다 더 좋은 필터링 결과를 얻을 수 있습니다.

 

 

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.