다운샘플링 (Downsampling)

sampling rate을 변환하는 이유가 뭔지 생각해보고 샘플링 속도를 줄이는 방법인 downsampling에 대해 알아봅시다. 

 

Sampling rate 변환

연속 시간 신호의 새로운 이산 시간 표현을 얻기 위해 이산 시간 신호의 샘플링 속도 (sampling rate)를 바꾸는 게 필요할 때가 있습니다. 샘플링 속도를 줄이는 작업을 downsampling, 올리는 작업을 upsampling이라고 합니다.

 

Downsampling

기존의 시퀀스에서 샘플을 뽑아내어 새로운 시퀀스를 정의해줌으로써 샘플링 속도를 줄일 수 있습니다. 

 

 

$M$은 integer factor 입니다. $M$이 2라면 짝수 번 (even)째 값만 취하고 홀수 번 (odd)째 값은 버리게 됩니다. $M$이 3이라면, 3의 배수 번째 값만 취하게 됩니다. 이렇게 일정한 주기로 값을 선택해서 뽑고 나머지는 버리는 것을 decimation이라고 부릅니다. 

 

Downsampling 주파수 영역 표현

 

원 신호 $x[n]$의 DTFT와 다운샘플링한 신호 $x_d[n]$의 DTFT 식을 바탕으로, $X(e^{j\omega})$와 $X_d(e^{j\omega})$가 어떤 관계를 가지는지 알아보도록 하겠습니다. 

 

 

먼저, $X_d(e^{j\omega})$에서 $r$을 $i+kM$으로 치환하여 식을 정리해줍니다. 

 

 

$X_d(e^{j\omega})$ 식을 살펴보면, $x[n]$의 DTFT인 $X(e^{j\omega})$와 비슷한 꼴인 식을 포함하고 있는 것을 볼 수 있습니다. $X_d(e^{j\omega})$에 포함된 이 식은 $X(e^{j\omega})$에서 $\omega$ 대신 $(\omega-2\pi i)/M$을 넣은 것으로 해석할 수 있기에 위와 같은 관계식을 갖게 됩니다. 

 

식에서 알 수 있듯이, $X_d(e^{j\omega})$는 주파수 축이 $M$으로 스케일링되고 $2\pi$의 정수배 만큼 shift된 $X(e^{j\omega})$의 M개의 copy들로 구성되어 있습니다. 따라서, $X_d(e^{j\omega})$는 $2\pi$의 일정한 주기를 갖는 걸 알 수 있습니다.

 

Aliasing을 방지하기 위해서 두 가지 조건을 만족해야 합니다. 첫 번째로, $X(e^{j\omega})=0$, $\omega_N\leq|\omega|\leq\pi$, 신호가 bandlimited 해야 합니다. 두 번째로,  $2\omega_N\leq2\pi/M$, 신호의 최대 주파수의 2배 보다 샘플링 주파수가 더 커야 하는 '나이퀴스트 샘플링 이론'을 만족해야 합니다. 

 

 

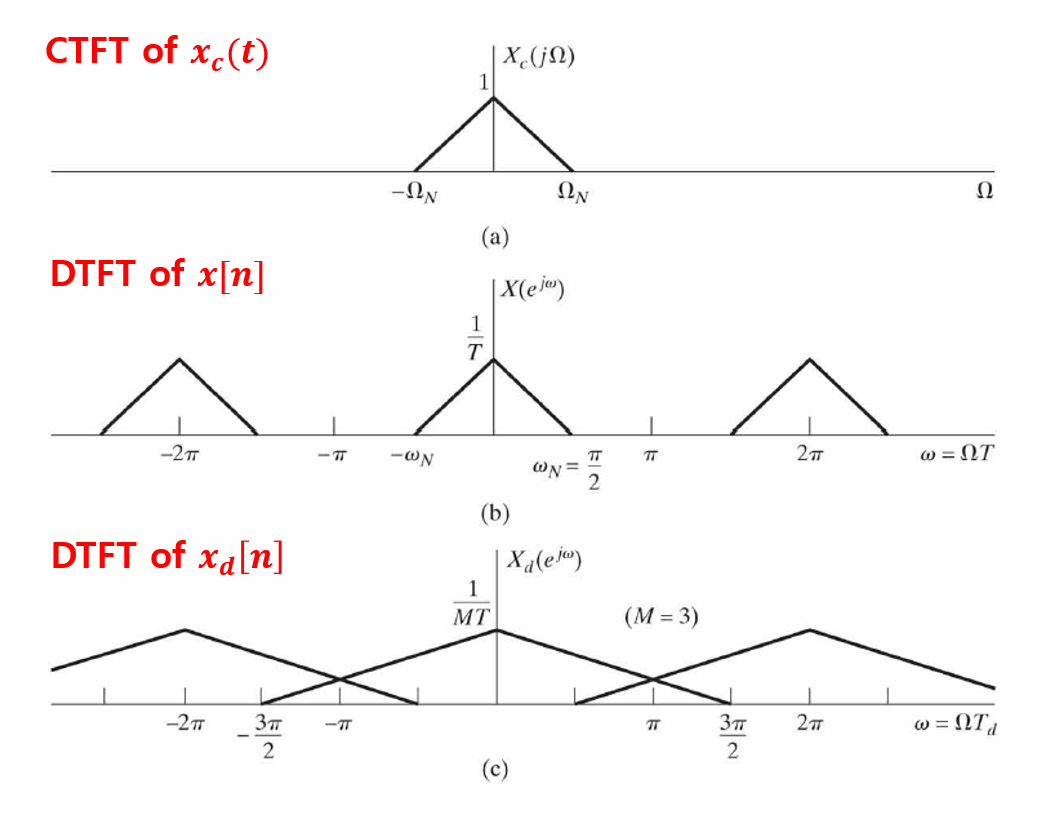
* Aliasing이 발생하지 않는 경우

 

오른쪽은 $M=2$ 인 경우, decimation한 신호 $x_d[n]$의 DTFT 결과를 나타낸 것으로 각각 이산 시간 주파수 $\omega$와 연속 시간 주파수 $\Omega$를 가로축으로 설정한 그림입니다. 기존의 신호와 비교했을 때, $x_d[n]$의 DTFT 결과를 보면 주파수 축이 2배가 늘어난 것을 볼 수 있습니다. 스펙트럼이 2배 넓어진 것처럼 보이지만 실제로 주파수 성분은 원 신호와 같습니다.

 

 

* Aliasing이 발생하는 경우

 

$M=3$ 인 경우, decimation한 신호 $x_d[n]$의 DTFT를 보면 고주파가 넘어와서 저주파 대역에 나타나는 aliasing 현상이 발생한 것을 볼 수 있습니다. Aliasing은 downsampling하기 전에 low-pass filter를 적용하여 주파수 대역을 제한함으로써 방지할 수 있습니다. 

 

Pre-filtering 후 Downsampling 적용

 

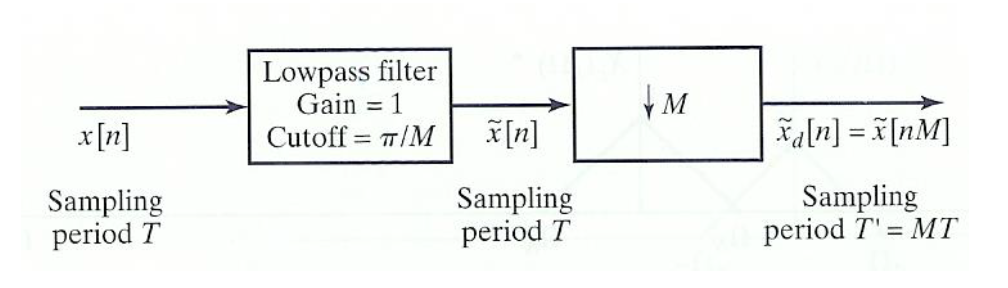
앞에서 봤듯이 downsampling으로 인해 aliasing이 발생한다면, downsampling 적용 전에 신호 $x[n]$의 대역폭 (bandwidth)을 줄여줘야 합니다. 이 작업은 샘플링 주기가 $T$인 신호 $x[n]$에 차단 주파수 (cutoff frequency)가 $\pi/M$인 anti-aliasing LPF를 적용함으로써 수행됩니다. 이렇게 사전 필터링을 통해 얻은 신호 $\tilde{x}[n]$을 이용하면, aliasing이 발생했던 $M=3$ 인 경우에도 주파수 간 overlap이 발생하지 않게 됩니다. 주파수 영역에서 다시 한 번 살펴보도록 하겠습니다.

 

 

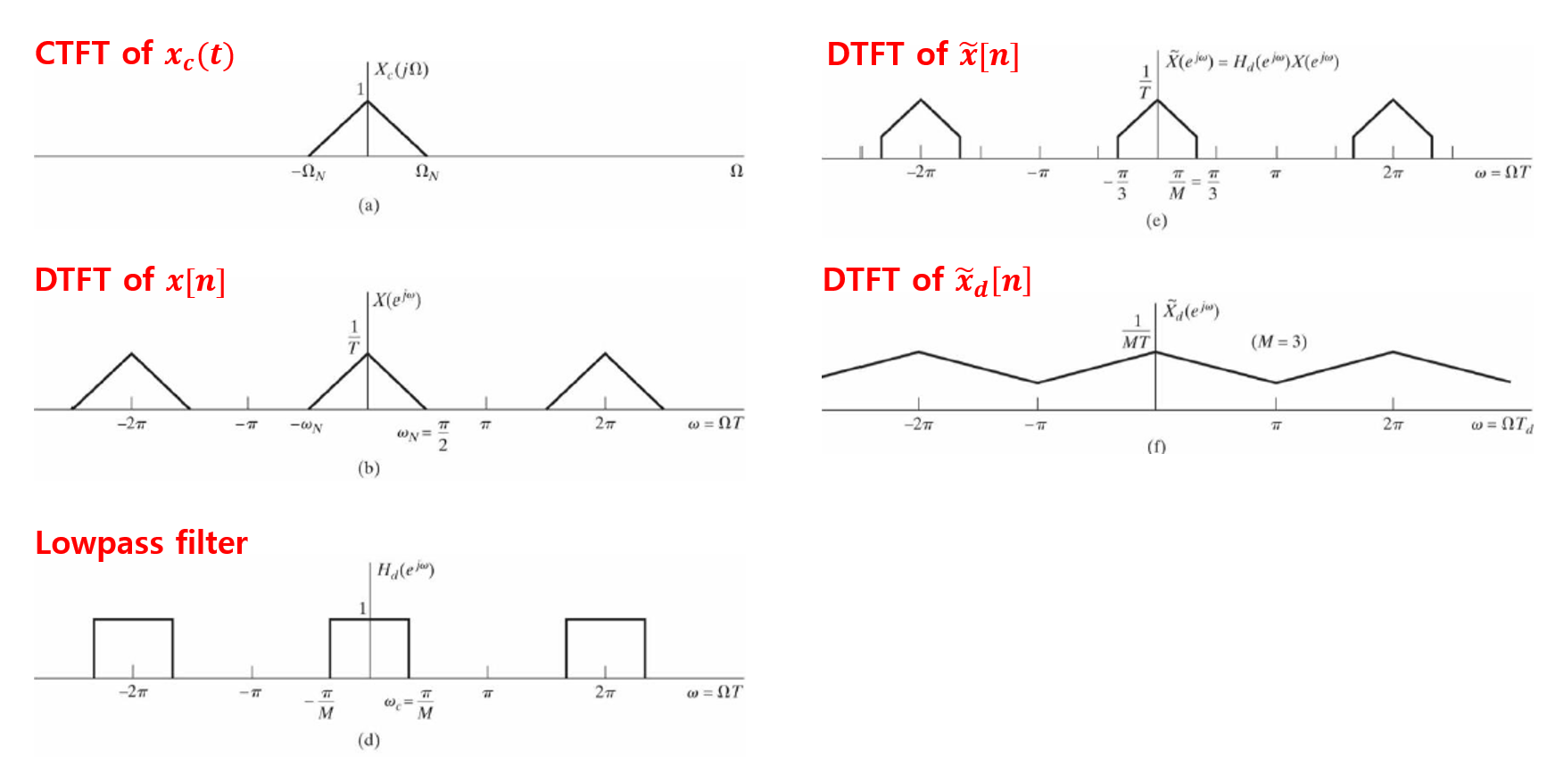
사전 필터링 작업 후 downsampling된 신호 $\tilde{x}_d[n]$의 DTFT 결과에 aliasing이 발생하지 않는 걸 확인할 수 있습니다!

 

 

GIST 신종원 교수님 '디지털신호처리' 수업 자료를 바탕으로 쓴 글입니다.