샘플링 이론 (Sampling Theorem) 알아보기

나이퀴스트 샘플링 이론에 대해 알아보고 연속 시간 신호를 샘플링하여 이산 시간 신호로 만드는 과정을 살펴봅시다.
 

Notation

 

Periodic Sampling

연속 시간 신호의 이산 시간 표현을 얻을 때 쓰는 일반적인 방법에는 periodic sampling이 있습니다. 말 그대로 일정한 주기로 샘플을 뽑아내는 작업을 뜻합니다.
 

 
여기서 $T$는 sampling period를 나타냅니다. $f_s=1/T$는 sampling frequency (단위: smaple/sec)를 의미하고 $\mathrm{\Omega }=2\pi /T$는 angular frequency (단위: radian/sec)를 나타냅니다. 
 

 
샘플링을 수학적으로 표현해보겠습니다. 주기적인 임펄스 트레인 $s(t)$를 연속 시간 신호 $x_c(t)$에 곱해 $x_s(t)$라는 modulation된 신호를 구할 수 있습니다. 델타 함수의 sifting property를 이용해 연속 시간 신호에서 $nT$ 간격으로 샘플을 뽑아 $x_s(t)$를 얻은 후 이 신호를 이산 시간 시퀀스로 표현해주면 $x[n]=x_c(nT)$가 됩니다.
 

샘플링의 frequency-domain 표현

 

$$X_s(j\mathrm{\Omega })=\frac{1}{T}\sum _{-\mathrm{\infty }}^{\mathrm{\infty }}{X}_c(j(\mathrm{\Omega }-k{\mathrm{\Omega }}_s))$$
 이 식은 연속 시간 신호 $x_c(t)$와 샘플링한 신호 $x_s(t)$ 각각을 푸리에 변환했을 때 관계를 보여줍니다. 
 

 
Bandlimited Signal $x_c(t)$의 푸리에 변환이 $X_c(j\mathrm{\Omega })$라고 할 때, $X_s(j\mathrm{\Omega })$는 $X_c(j\mathrm{\Omega })$ 꼴이 주기적으로 반복되고 크기가 스케일링된 copy들을 모아놓은 형태로 나오는 걸 확인할 수 있습니다. 또한, $X_s(j\mathrm{\Omega })$의 copy들은 sampling frequency인 ${\mathrm{\Omega }}_s$의 정수배 만큼 shift 돼 있는 걸 볼 수 있습니다.
 

샘플링 이론 (Sampling Theorem)

나이퀴스트 (Nyquist) 이론에 따르면, 샘플링 시 aliasing이 일어나지 않으려면 연속 시간 신호가 가진 최대 주파수 성분의 2배 이상으로 샘플링 주파수 (sampling frequency)를 설정해야 합니다. 다시 말해, 위 조건을 만족해야 이산 시간 신호를 본래의 연속 시간 신호로 복원할 수 있습니다. 
 
간단한 예시를 살펴보겠습니다. 위 그림처럼 신호 $x_c(t)$의 푸리에 변환인 $X_c(j\mathrm{\Omega })$가  bandlimited 하다고 가정해봅시다.
 
$$|X_c(j\mathrm{\Omega })|=0,|\mathrm{\Omega }|>{\mathrm{\Omega }}_N$$

 
샘플링 조건을 만족할 때, 등간격 ($n{T}_s$)으로 뽑은 샘플들로 이루어진 이산 시간 시퀀스 $x[n]$을 통해 연속 시간 신호 $x_c(t)$를  복원할 수 있습니다. 여기서 ${\mathrm{\Omega }}_N$은 신호의 최대 주파수로 Nyquist frequency이라 불리고 2${\mathrm{\Omega }}_N$은 신호를 복원하기 위한 최소 sampling rate로 Nyquist rate라고 불립니다. 
 

 
위 샘플링 이론에 따르면, 신호의 최대 주파수를 나타내는 ${\mathrm{\Omega }}_N$의 2배보다 샘플링 주파수 ${\mathrm{\Omega }}_s$가 더 크면 aliasing이 발생하지 않습니다. 반대로, ${\mathrm{\Omega }}_N$의 2배보다 샘플링 주파수가 더 작으면 샘플링된 신호를 푸리에 변환한 $X_s(j\mathrm{\Omega })$에서 복제된 스펙트럼이 중첩되는 현상인 aliasing이 발생하게 됩니다.  전자의 경우, ideal low-pass filter를 통해 연속 시간 신호 $x_c(t)$를 복원할 수 있습니다. 하지만, 후자의 경우 중첩으로 인해 샘플들 간 왜곡이 일어났기 때문에 연속 시간 신호를 제대로 복원할 수 없게 됩니다. 
 

 
${\mathrm{\Omega }}_s>2{\mathrm{\Omega }}_N$인 경우 (aliasing 발생 X), 연속 시간 신호를 복원하는 과정을 나타낸 그림입니다. 샘플링된 신호를 푸리에 변환하여 얻은 스펙트럼 copy를 gain 값이 $T$인  low-pass filter를  적용하여 원하는 부분만을 추출해 복원된 신호 $X_r(j\mathrm{\Omega })$를 출력하는 걸 확인할 수 있습니다. 
 

이산 시간 푸리에 변환 (Discrete-time Fourier Transform, DTFT)

 
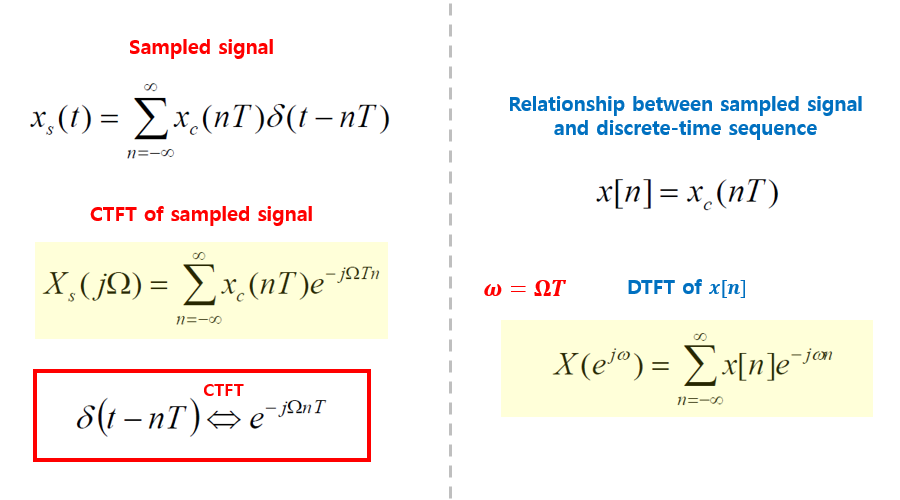
샘플링된 신호 $x_s(t)$의 CTFT 식과 $x[n]$의 DTFT 식을 비교해보면, $\omega =\mathrm{\Omega }T$인 경우에  같은 식이 되는 것을 알 수 있습니다. 
 

 
$\omega =\mathrm{\Omega }T$ 관계식을 바탕으로, $X(e^{j\omega })$는 주파수 축이 스케일링된 $X_s(j\mathrm{\Omega })$로 해석할 수 있습니다. 이렇게 스케일링 해주는 이유는.. $X_s(j\mathrm{\Omega })$의 주파수 성분 $\mathrm{\Omega }={\mathrm{\Omega }}_s$가 $X(e^{j\omega })$의 $\omega =2\pi$에 매핑되도록 주파수 축을 정규화 (normalize) 하기 위해서입니다.
 
$$\mathrm{\Omega }=\frac{\omega }{T}{\mathrm{\Omega }}_s=\frac{2\pi }{T}$$
 
GIST 신종원 교수님 '디지털신호처리' 수업 자료를 바탕으로 쓴 글입니다.
 

Reference

[1] “[신호 처리] 2. '샘플링(sampling)'의 의미와 적절한 샘플링 율(sampling rate) 설정 방법 / sampling theorem / 에일리어싱(Aliasing)발생 이유,” 비전공자 데이터분석 노트, Mar. 09, 2023. https://bigdaheta.tistory.com/89 (accessed Apr. 08, 2024).
‌