LTI 시스템의 주파수 응답과 phase distortion, group delay

LTI 시스템의 frequency response에 대해 알아보고 phase distortion, group delay 개념을 살펴봅시다.

 

LTI 시스템의 frequency response

시스템의 주파수 응답 (frequency response)이 선형 시불변 시스템 (LTI system)을 특징짓듯이, 임펄스 응답 (impulse response)을 알면 LTI system 전체를 이해할 수 있게 됩니다.

 

 

• LTI system: linearity와 time-invariant 속성을 가진 시스템
• impulse response: 시간 영역에서 LTI 시스템의 입출력 성질을 보여줌, 입력으로 임펄스가 들어왔을 때 시스템의 출력
• frequency response: 주파수 영역에서 LTI 시스템의 입출력 성질을 보여줌
• transfer function: 복소주파수 영역에서 LTI 시스템의 입출력 성질을 보여줌

 

임펄스 응답의 z변환은 $H(z)$로 표기되며, 전달 함수 (transfer function 또는 system function)이라고 부릅니다.

 

 

주파수 응답 $H(e^{j\omega})$은 ROC가 $|z|=1$ (unit circle)을 포함하는 경우에 값을 가지기 때문에, 다음 조건을 만족해야 합니다.

 

$$H(e^{j\omega})=H(z)|_{|z|=1}$$

 

 

입력 신호의 DTFT 결과와 주파수 응답이 주어졌다고 가정해봅시다. 각각 phase와 magnitude 정보를 가지고 있는데 이 값을 활용하여 LTI 시스템 출력의 magnitude와 phase를 구해줄 수 있습니다. 이렇게 magnitude와 phase response를 기반으로 LTI 시스템을 모델링하고 분석할 수 있습니다.

 

Phase Ambiguity (위상 모호성)와 Principle value

주파수 응답에서 phase는 주파수 $\omega$에 따라 변화합니다. 위상 (phase)은 $2\pi$의 정수배 간격으로 값이 동일해지기 때문에 주파수 영역 상 phase 값은 유일하지 않습니다. 이러한 현상을 phase ambiguity라고 합니다.

 

 

앞서 말했듯이, phase는 주기적인 성질을 갖고 있기 때문에 위상이 0부터 $2\pi$ 범위에서만 유일하게 정의됩니다. 그렇기 때문에, $2\pi$의 정수 배를 빼줘서 $-\pi$부터 $\pi$까지의 범위로 wrapping하여  principle value로 바꿔줍니다.

 

• phase wrap-around (wrapping): 일정 범위를 벗어나면 다시 해당 범위 내로 돌아가도록 제한된 범위에서 위상 표현
• phase unwrapping: 위상 값을 보정하여 다시 연속적인 위상 곡선을 얻는 과정

 

phase의 principle value는 $ARG[H(e^{j\omega})]$로 표기됩니다. 시스템의 phase response는 principle value $ARG[H(e^{j\omega})]$와 integer $r(\omega)$에 $2\pi$를 곱한 값을 더해준 식으로 정의됩니다. 

 

 

그림을 통해 다시 한번 살펴 보겠습니다. 컴퓨터가 처리할 수 있는 이산적인 값으로 나타내주기 위해, 연속적인 phase 정보 $arg[H(e^{j\omega})]$를 $-\pi$부터 $\pi$까지 $2\pi$의 한정 (bounded)된 범위로 정의합니다. 이후, 다시 연속적인 값으로 만들어 주고자 할 때, $r(\omega)$를 정의해야 하는데.. 일반적으로 정확한 integer 값을 알 수 없기 때문에 원래 phase 값을 복원하기 어렵다고 합니다.

 

Group Delay

 

group delay는 phase response를 주파수 $\omega$에 대해서 미분한 값에 negative를 취한 값으로 정의됩니다. (미분할 때 phase가 unwrapping되어 있어야 합니다!) 

 

group delay 값이 상수라는 것은 모든 주파수가 똑같은 delay를 가지는 것 (phase가 linear하거나 0)을 의미합니다. 다시 말해, 여러 신호들의 입출력 순서는 똑같고 그저 phase만 shift 된 형태로 나타나게 됩니다. 반대로, group delay 값이 일정하지 않고 계속 변화한다면, nonlinear한 속성으로 인해 시스템 분석이 어려워집니다. 

 

 

3개의 신호의 phase spectrum과 group delay를 나타낸 그림입니다. 노란색 signal을 보면 phase가 $2\pi$ 주기로 반복되는 걸 볼 수 있습니다. 또한, 각각의 신호의 주파수 응답의 크기 (gain)이 0이 되는 지점에서, 위상이 빠르게 변화하기 때문에 상대적으로 sample delay가 작은 음수 값을 가지는 걸 확인할 수 있습니다.

 

phase distortion과 delay

 

Ideal delay system 예시를 살펴보겠습니다. group delay가 $n_d$이므로 선형 위상 (linear phase) 속성을 갖는 ideal low-pass filter는 아래와 같이 정의됩니다. 

 

 

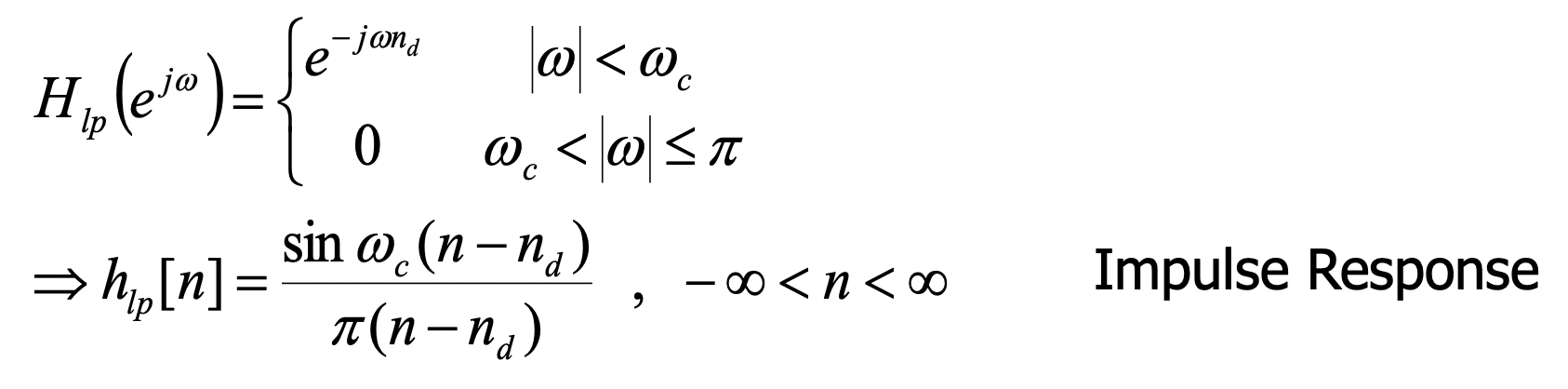
* zero phase

만약 phase 값이 0으로 정의된다면, phase를 주파수로 미분하여 negative를 취한 값인 group delay도 0 (신호의 시간 지연 X)이 되기 때문에 임펄스 응답은 $n=0$을 중심으로 자리하게 됩니다. 결과적으로, 현재의 입력에 대해 과거의 response 값이 존재하게 되는데 이는 곧 과거의 response가 현재의 입력에 영향을 받게 된다는 걸 의미합니다. 따라서, 이 시스템은 non-causal 하며 실시간 (real-time)으로 구현될 수 없습니다.

 

+) 어떤 시점을 기준으로 미래 값을 참조하고 있다면 non-causal 함

 

 

 

* linear phase

 

 

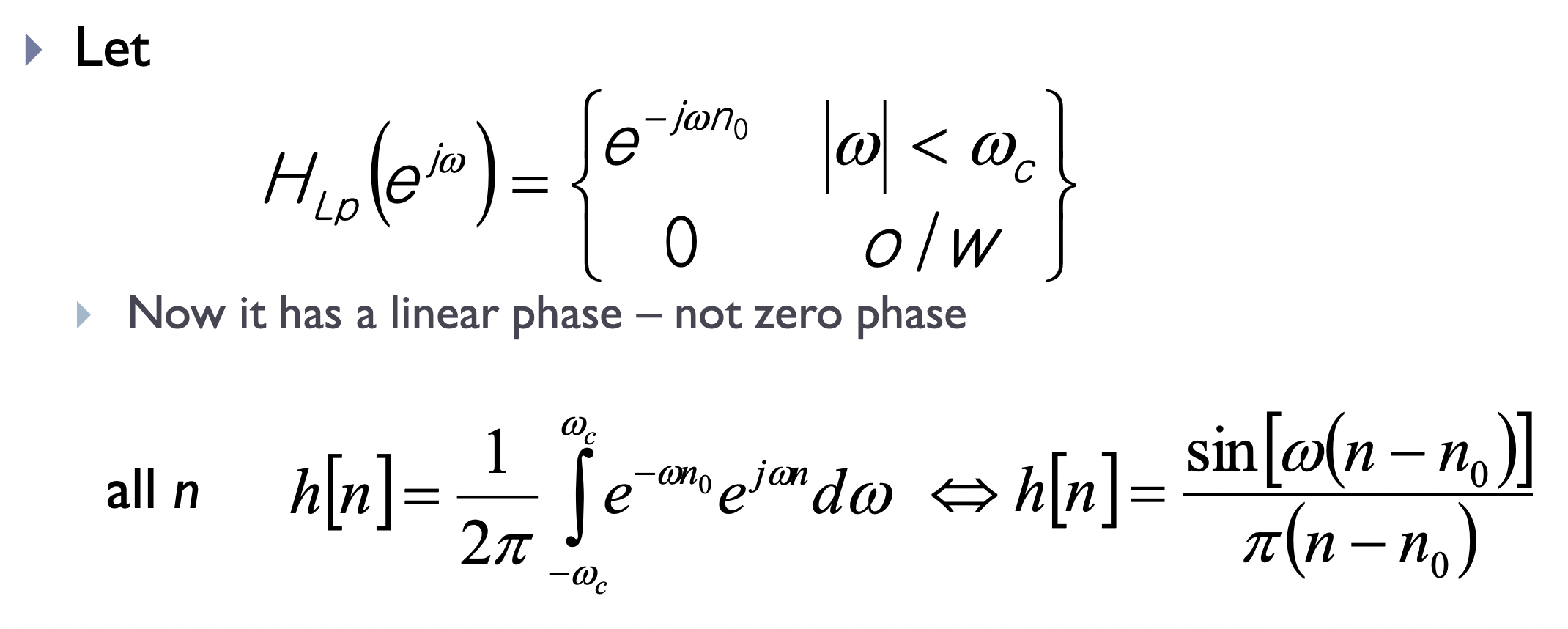
이번에는 time delay가 $n_0$인 delay system 예시를 살펴보겠습니다. linear phase를 갖는 이 시스템에서의 위상은 주파수에 따라 일정한 변화가 나타납니다. 이는 주파수 영역 상, 입력 신호의 모든 주파수 성분에 동일한 시간 지연이 적용된다는 것을 의미합니다. 그렇기 때문에, 선형 위상 왜곡 (linear phase distortion)은 입력 신호를 균일하게 지연 (time delay)시키는 것으로 해석할 수 있겠습니다. 다시 말해, non-causal한 zero phase 시스템에 delay를 $n_0$ 만큼 적용함으로써 causal한 linear phase 시스템을 만들 수 있습니다.

 

 

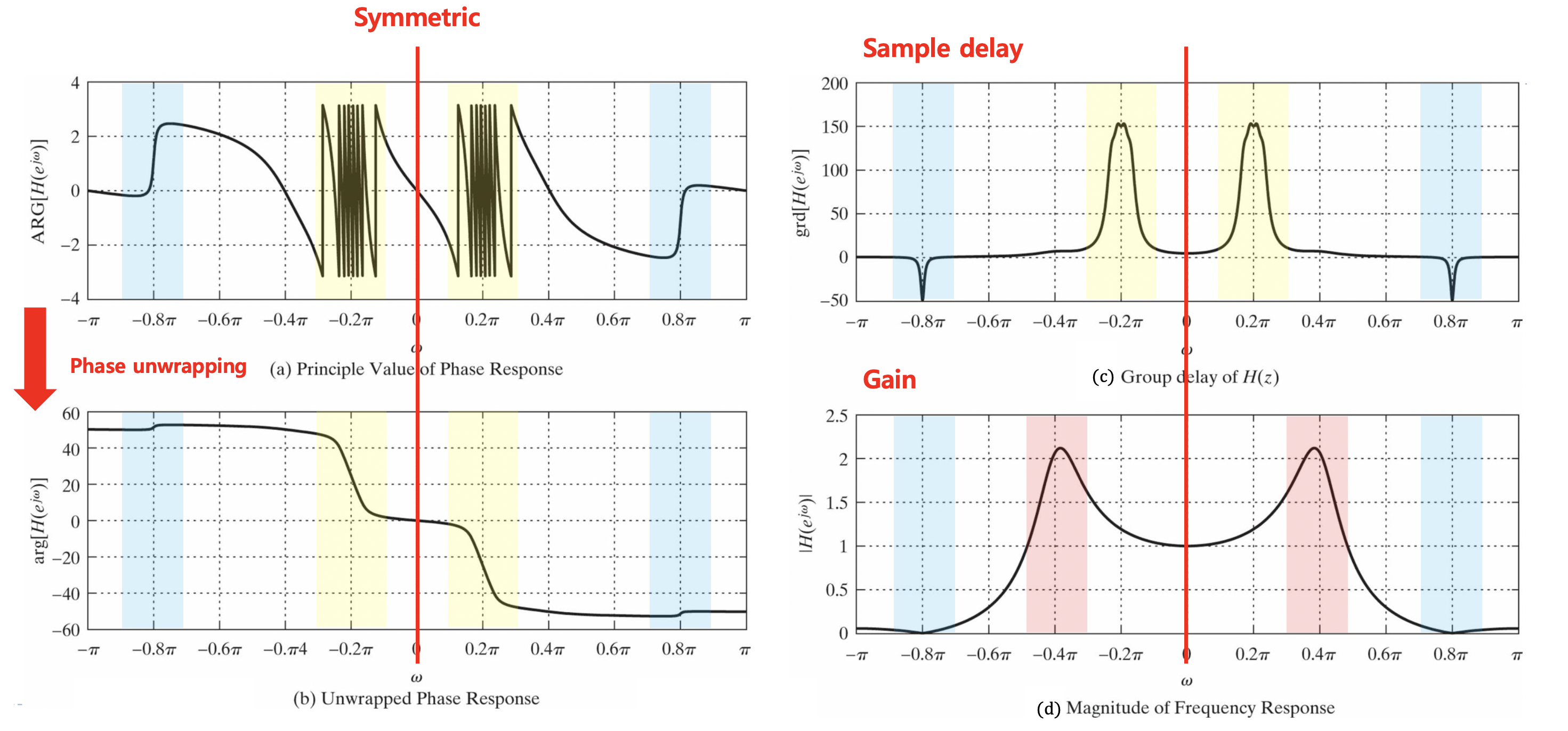
Group delay가 신호에 어떤 영향을 미치는지 그림을 통해 알아보겠습니다. (a)는 Phase response의 principle value를 나타낸 것으로, 이를 unwrapping 시켜주면 일정한 범위로 매핑되어있던 phase 값이 그림 (b)와 같이 연속적인 형태로 나오게 됩니다. (a), (b)를 비교해보면 전체적으로 phase가 빠르게 변하거나 거의 변화가 없이 일정한 양상이 비슷하게 나타나는 걸 확인할 수 있습니다. 또한, (d)의 gain이 0이 되는 지점 ($\pm0.8\pi$)에서 급격한 phase 변화가 일어나기 때문에 (c)의 같은 지점에서 group delay 값이 작은 음수 값을 갖게 됩니다.

 

(c) group delay 그림을 보면, $\pm0.2\pi$에서 150 샘플, $\pm0.4\pi$에서 10샘플 정도 딜레이 되는 걸 알 수 있습니다. (d) magnitude 그림에서는 $\pm0.2\pi$의 gain은 1.2배 정도 증가하고 $\pm0.4\pi$에서는 2배 가까이 증가하며 $\pm0.8\pi$에서는 gain이 0이라는 걸 확인할 수 있습니다.  phase, magnitude 그리고 group delay에 따라 결과값이 어떻게 나타나는지 예시를 살펴보도록 하겠습니다.

 

 

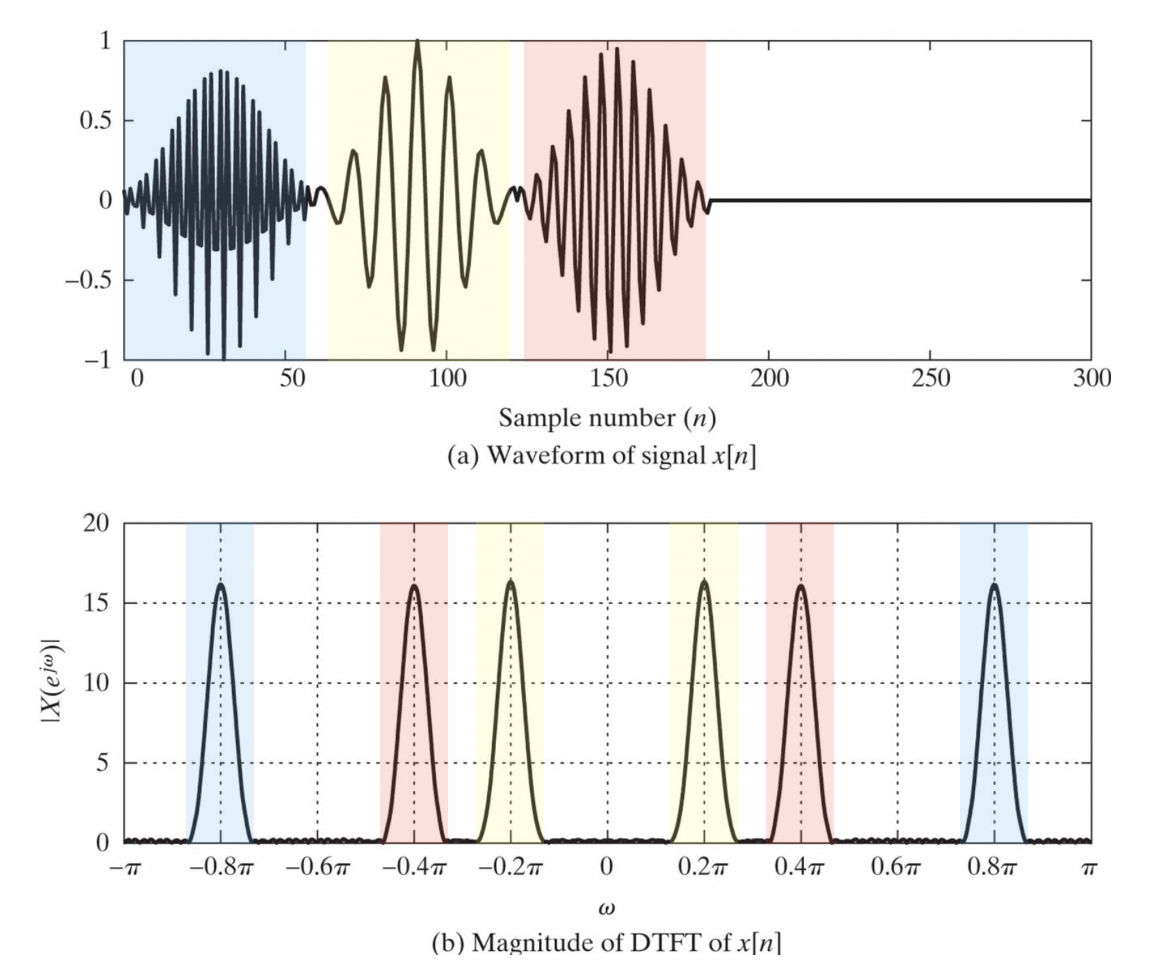
3개의 신호 (정확히는 여러 주파수 신호로 이루어져 있겠지만..)를 DTFT한 결과가 $\pm0.2\pi$, $\pm0.4\pi$, $\pm0.8\pi$에서 나타난다고 가정해봅시다. 

 

 

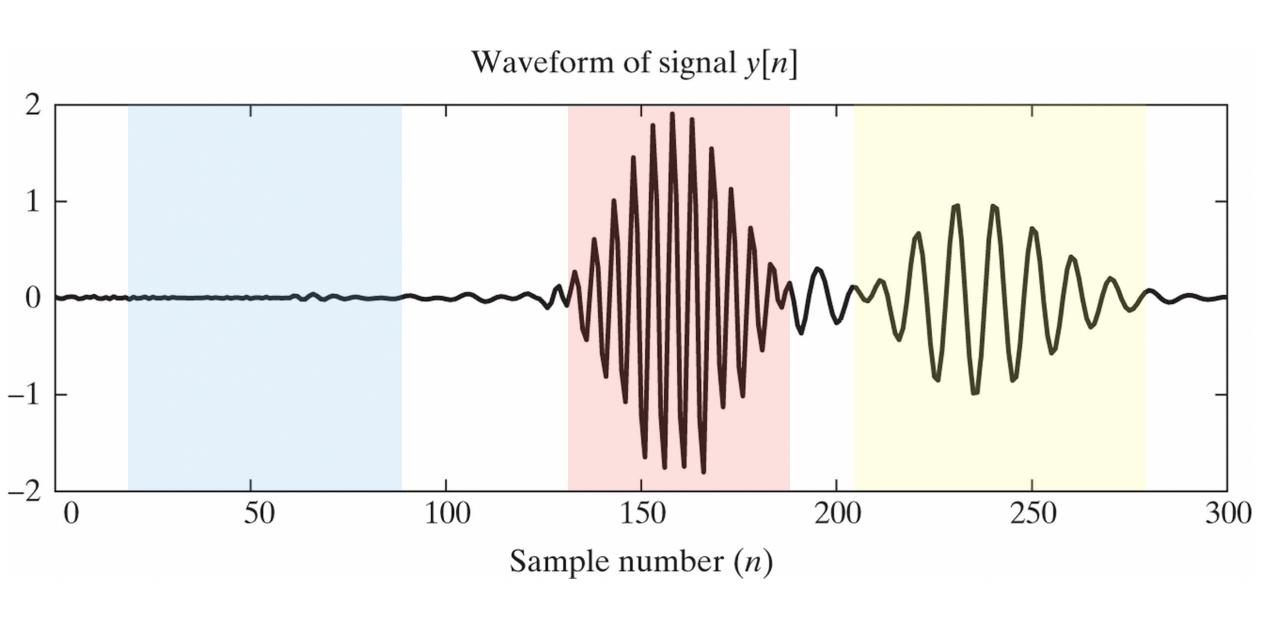
group delay와 gain을 적용하면 위와 같이 나오게 됩니다. $\pm0.8\pi$ 지점에서 gain이 0이기 때문에 신호가 거의 감쇠된 걸 확인할 수 있고 반대로 $\pm0.2\pi$ 지점에서는 gain이 2배 증가한 걸 볼 수 있습니다. 또한, $\pm0.2\pi$에서 150 샘플, $\pm0.4\pi$에서 10샘플 정도 딜레이된 것도 알 수 있습니다.

 

 

GIST 신종원 교수님 '디지털신호처리' 수업 자료를 바탕으로 쓴 글입니다.