Gradient Descent를 위한 최적화 알고리즘

목차

1. Stochastic gradient descent (SGD)

2. Momentum

3. Nestrov accelerated gradient (NAG)

4. Adagrad

5. RMSProp

6. Adadelta

7. Adam

8. Adamax

9. Noam decay

10. Cosine Annealing with Warm Restart

 

---

1. Stochastic gradient descent (SGD)

 

Gradient Descent 알고리즘은 오류 함수의 기울기(미분)를 계산해 이를 바탕으로 파라미터를 업데이트하여 최적점을 찾는 방법입니다. Gradient Descent에는 두 가지 방식이 있는데, Steepest Descent 알고리즘은 전체 데이터를 사용해 기울기를 계산하는 반면, Stochastic Gradient Descent (SGD) 알고리즘은 데이터의 부분집합(mini-batch)을 사용한다는 차이점이 있습니다. Steepest Descent 알고리즘은 정확하지만 데이터가 클 경우 계산량이 많다는 문제를 가지고 있는데 이를 완화하기 위해 SGD는 소량의 샘플만을 가지고 기울기를 계산합니다. 

 

• saddle point: gradient가 0인 지점으로, 일부 방향에서는 최솟값처럼 보이지만 다른 방향에서는 최댓값처럼 보임

하지만, SGD도 적절한 learning rate 설정이 어렵다는 문제가 있습니다. 그리고 learning rate를 조정할 때, 특정 조건이나 반복 횟수에 따라 변경할 기준을 미리 설정해야 합니다. 또한, learning rate가 scalar일 경우 모든 파라미터에 동일한 값이 적용되는 게 비효율적일 수 있으며 saddle point로 인해 최적점인 global minima를 추정하지 못하는 등 정확한 계산이 어려울 수 있습니다.

 

2. Momentum

 

gradient가 0인 saddle point에 갇히면 더 이상 파라미터가 업데이트되지 않습니다. saddle point에서 탈출하고 최적점에 빨리 수렴하도록 SGD를 보완하기 위해, Momentum이 등장했습니다. Momentum은 단순히 현재 기울기만 따르는 게 아니라, 최근에 계산된 gradient 값의 평균치를 바탕으로 원래 가던 방향에 더 가중치를 주는 방법입니다. momentum term $\gamma$는 이전 이동 방향을 반영하여 수렴 속도를 높이는 역할을 수행하며 값이 $0$인 경우, SGD와 동일해집니다. 일반적으로 $\gamma$는 0.9로 설정됩니다.

 

3. Nestrov accelerated gradient (NAG)

 

NAG는 momentum과 유사하지만, gradient가 현재 파라미터값과 momentum term을 더한 값으로 계산됩니다. 이 값은 업데이트된 파라미터의 근사값으로 활용됩니다. 

 

4. Adagrad

 

Adagrad는 파라미터 벡터 $\theta$의 각 component마다 다른 learning rate를 적용하기 위해 고안되었습니다. 이미 업데이트가 많이 된 파라미터는 더 작은 learning rate를 사용하여 업데이트 속도를 늦춥니다. 이 방법은 자주 발생하는 feature와 드물게 있는 feature가 존재하는 application에 유용합니다. 고정된 learning rate ($\mu=0.01$)를 가지고 대부분 잘 동작하지만, $G_k(n)$ 값이 시간에 따라 커지면서 업데이트량이 작아지기 때문에 nonstationary 데이터 처리에는 바람직하지 않을 수 있습니다. 또한, initial gradient가 큰 값이면 전체 학습 과정이 느려지는 등 initialization에 민감합니다.

 

5. RMSProp

 

RMSProp은 Adagrad에서의 $G_k(n)$을 단순히 accumulation하는 게 아닌 forgetting factor를 도입한 recursive averaging 방식으로 바꿨습니다. Adagrad의 경우 초기 업데이트량이 많으면 계속해서 작은 learning rate가 부여되는데 RMSProp은 시간이 많이 지난 상태면 다시 업데이트량을 늘립니다. 

 

6. Adadelta

 

SGD나 momentum 알고리즘에서 cost function이 unit이 없고 (무차원), 파라미터가 가정된 unit을 가지고 있다면, 파라미터 업데이트 unit은 해당 파라미터 unit의 역수가 됩니다. Adagrad에서는 업데이트 unit이 무차원 값이 되지만, Adadelta에서는 파라미터 업데이트 unit이 파라미터 자체 unit과 동일합니다. 이 가정은 classification에 많이 사용되는 cross-entropy 같은 cost function에는 적합하지만, regression task에서 쓰이는 mean square error 같은 cost function에는 적합하지 않을 수 있습니다.

 

 

7. Adam

 

Adam은 각각의 파라미터에 대해 1차 moment (gradient average)과 2차 moment (gradient square average) 값을 추적하여 learning rate을 adaptive하게 조정합니다. $v_k(n)$은 1차 moment 추정값으로 gradient의 exponential moving average 입니다. $G_k(n)$은 2차 moment 추정값으로, gradient 제곱에 대한 exponential moving average 입니다. 초깃값이 0이므로, 첫 몇 번의 업데이트 동안에는 $v_k$와 $G_k$ 값이 편향되어 작은 값을 가질 수 있습니다. 이 문제를 해결하기 위해, 위와 같이 보정 과정을 거칩니다. 최종적으로 각 파라미터는 보정된 moment 값을 이용하여 업데이트됩니다. 

 

8. Adamax

 

Adam 알고리즘에서는 파라미터 업데이트가 이전과 현재 gradient의 $l_2$ norm에 반비례합니다. 이 개념을 일반화하여 $l_p$ norm으로, 그리고 $l_\infty$로 표현하여 파라미터 업데이트 식을 위와 같이 새롭게 정의해줄 수 있습니다.

 

9. Noam decay

 

Noam decay는 Transformer에서 사용되는 learning rate schedule입니다. Adam optimizer를 기반으로 learning rate $\mu$ 값을 결정합니다. $N_w$는 warmup step을나타내는데 학습 초기에 learning rate를 증가시키는 구간을 나타냅니다. warmup 구간 동안 learning rate는 선형적으로 증가하며 warmup이 끝나면 learning rate는 step number $n$의 역제곱근에 비례하여 감소합니다. 학습 초반에는 learning rate를 천천히 높여가고, 그 이후로는 learning rate를 줄여감으로써 효율적이면서 안정적으로 모델이 학습할 수 있도록 도와줍니다. 

 

10. Cosine Annealing with Warm Restart

 

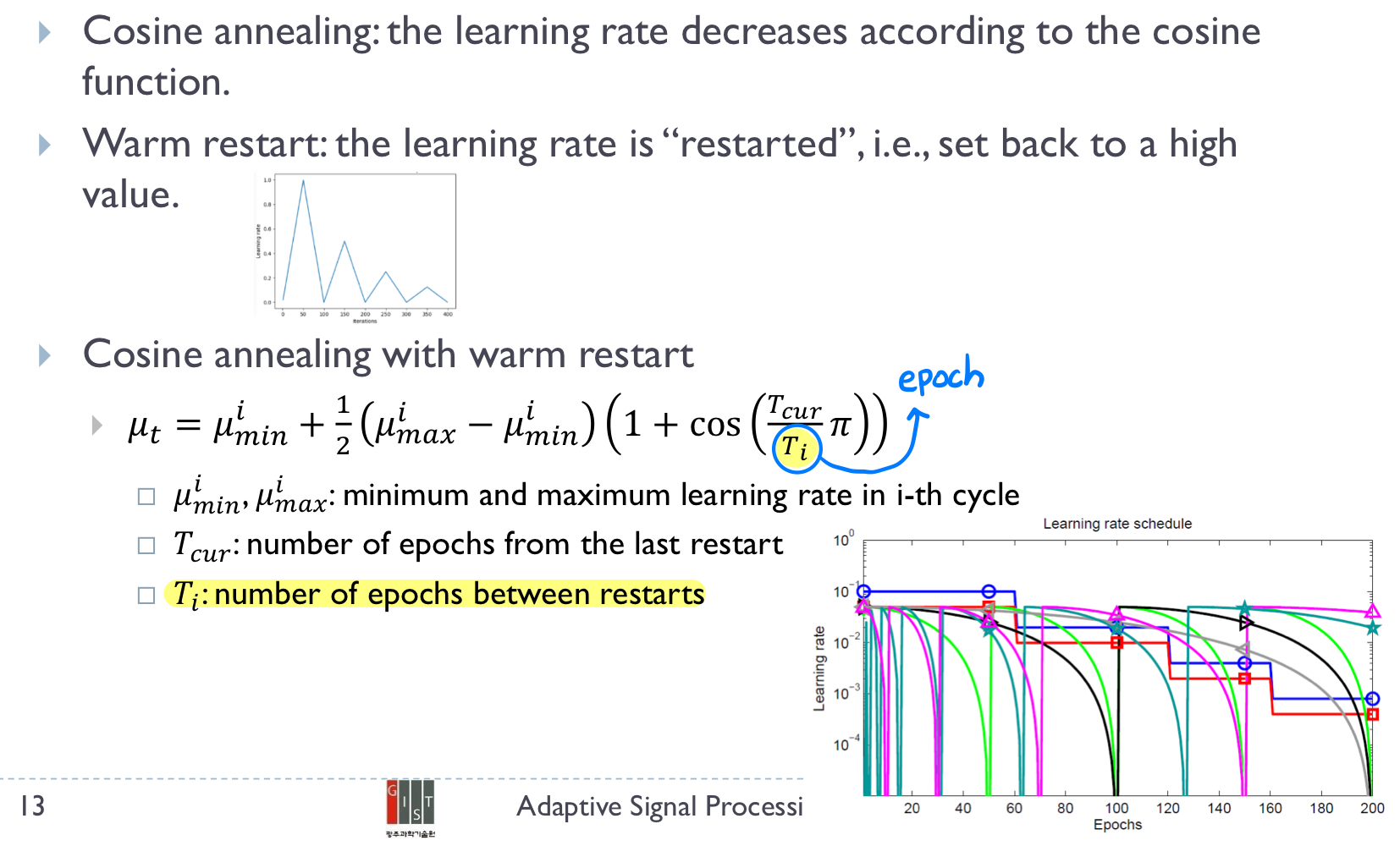
Consine Annealing은 학습이 진행됨에 따라 learning rate가 cosine 함수 형태로 감소하다가, 주기적으로 높은 값으로 다시 리셋 (warm restart)되는 방식입니다. local minima에 갇혀도 warm restart를 통해 특정 learning rate 값으로 돌아감으로써 탈출할 수 있습니다. 

GIST 신종원 교수님 '적응신호처리' 수업 자료를 바탕으로 쓴 글입니다.