DFT (Discrete Fourier Transform) 바로 알기

이산 푸리에 변환 (DFT)의 정의와 특성, 그리고 중요한 개념인 circular convolution에 대해 알아보고 예제를 통해 개념을 정리해봅시다. 

 

DFT를 쓰는 이유

DFS (Discrete Fouirer Series)는 신호가 주기적인 성질을 가진다고 가정하고, 이를 이산 시간 신호의 주파수 영역 표현으로 변환합니다. 주파수 축에서는 이산적인 값으로 나오지만, 만약 신호가 주기적이지 않을 경우에는 정확한 표현이 어려울 수 있다는 문제가 있습니다.

 

반면, DTFT(Discrete-Time Fourier Transform)는 주기성과 무관하게 모든 시간 영역 신호를 주파수 영역으로 변환할 수 있습니다. 하지만, DTFT 결과는 주파수 축에서 연속적인 값으로 나오기 때문에, 이산적인 정보만을 처리할 수 있는 컴퓨터에서는 직접 처리하기 어렵습니다.

 

이 문제를 해결하기 위해. DFT (Discrete Fourier Transform)는 유한한 길이의 신호를 가정하고, 주파수 축을 샘플링하여 이산적인 형태로 주파수 값을 변환합니다. DFT는 본질적으로 DTFT에 주파수 샘플링을 적용한 것으로 볼 수 있으며, 이러한 성질 덕분에 DFT는 주파수 영역의 정보를 컴퓨터로 효과적으로 처리할 수 있습니다.

 

DFT와 DFS의 관계

 

$n$이 $0$ 부터 $N-1$ 범위 바깥에 존재한다면, $0$ 값을 갖는다고 가정해봅시다. 만약 $x[n]$의 전체 시퀀스 길이 $M$보다 DFT 길이인 $N$이 더 크다면, $x[n]$은 $M$ 부터 $N-1$ 범위에서 $0$값을 갖게 될 것입니다. $x[n]$의 주기적 확장을 위와 같이 $\tilde{x}[n]$이라고 정의하였을 때, 이 주기적인 성질을 갖는 시퀀스는 유한한 시퀀스 $x[n]$의 모듈러 연산으로도 나타낼 수 있게 됩니다. 

 

 

이러한 성질로 인해, DFT 계수 $X[k]$와 DFS 계수 $\tilde{X}[k]$는 위와 같은 관계식을 가집니다. DFT 계수는 DFS 계수의 한 주기를 나타내며, $N$ 이후 값들은 다시 $N$이전의 값들과 동일하게 반복됩니다. 

 

 

DFS의 경우, 주기적인 시퀀스를 가정하기 때문에, 범위를 지정할 필요가 없습니다. 그에 반해, DFT는 유한한 시퀀스를 가정하기 때문에 범위를 정해줘야 합니다. 

 

 

$0$부터 $4$까지 범위가 정해진 유한한 시퀀스 $x[n]$을 가정했을 때, 이를 주파수 영역으로 변환해보면 pulse가 총 $N=5$개 생기고 전체적으로 봤을 때 rectangular 모양으로 나타나는 것을 확인할 수 있습니다.

 

 

다음은, $N=10$일 때 $\tilde{X}[k]$를 구한 예제입니다. 같은 식이더라도, DFT 길이에 따라 값이 완전히 달라진 것을 확인할 수 있습니다.

 

DFT의 property

* Linearity / Circular Shift

 

시간 영역에서 circular shift는 주파수 영역에서 시퀀스의 DFT에 complex exponential을 곱한 것과 같습니다. 여기서 circular shift란 주파수 영역에서 주기적으로 확장된 신호의 phase shift를 말합니다. 

 

* Duality

 

* Symmetry Property

 

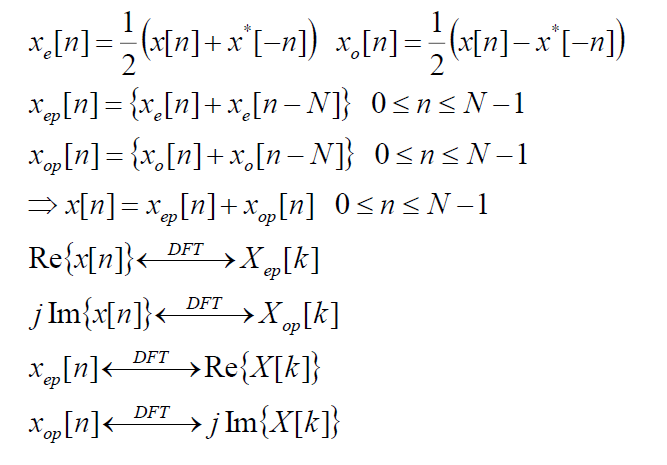
property 한 눈에 보기

 

Circular Convolution

frequency-domain

 

시간 영역에서의 컨볼루션은 주파수 영역에서 곱으로 나타나기 때문에 위와 같이 정의됩니다. DFT 계수인 $X_3[k]$를 다시 시간 영역 표현으로 바꿔준 컨볼루션 식은 아래와 같습니다. 

 

 

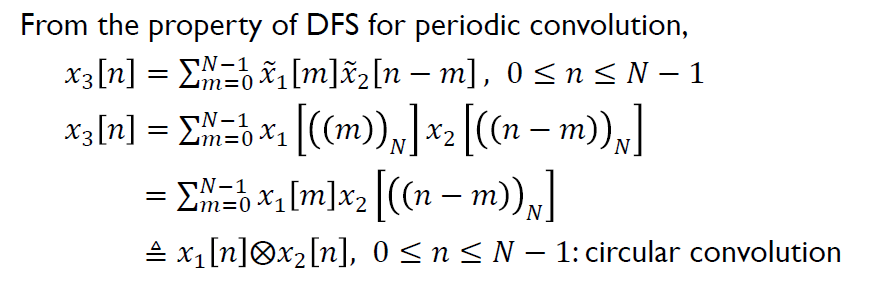
주기성을 갖는 시퀀스 ${\tilde{x}}_1[n]$과 ${\tilde{x}}_2[n]$의 circular convolution 결과인 $x_3[n]$을 보면, $x_1[n]$의 경우 $0$부터 $N-1$ 사이에 존재하기 때문에 modulo 연산을 수행할 필요가 없어 원래의 값을 그대로 쓰는 걸 볼 수 있고, $x_2[n]$의 경우 modulo shift를 하며 컨볼루션 연산을 수행하는 것을 확인할 수 있습니다.

 

DFS/DFT의 주기적 성질로 인해, circular convolution은 linear convolution과는 다른 방식으로 수행됩니다. 두 방법의 메커니즘이 어떻게 다른지 설명한 글을 첨부하였으니 참고하시면 좋을 듯 합니다 :)

 

선형 컨볼루션 (Linear convolution)과 원형 컨볼루션 (Circular convolution)

 

 

GIST 신종원 교수님 '디지털신호처리' 수업 자료를 바탕으로 쓴 글입니다.