일반적으로, 컴퓨터를 통해 신호를 분석하는데 DFT를 사용합니다. DFT는 DTFT의 주파수 영역 샘플로 filtering, spectral anlysis에 유용한데 왜 그런지 알아보겠습니다. 그리고 시간 영역에서의 windowing과 주파수 영역에서의 sampling이 DFT 결과에 어떤 영향을 미치는지 살펴보도록 하겠습니다.
DFT와 DTFT 간 관계

CTFT와 DTFT의 관계식이 위와 같을 때, 시퀀스 $x[n]$과 유한한 길이의 window $w[n]$ 간 곱은 $v[n]$으로 정의됩니다. $v[n]$의 DTFT는 아래와 같습니다.


$V[k]=V(e^{j\omega})|_{\omega=2\pi k / N}$ 식을 통해, DTFT를 fundamental frequency $\omega_0=2\pi / N$ 정수배로 샘플링한 것이 DFT라는 것을 알 수 있습니다.
Windowing과 spectral sampling이 DFT에 미치는 영향

그림을 통해 다시 한 번 살펴보겠습니다. 신호의 DTFT를 나타낸 그림 (d)와 DFT를 나타낸 그림 (f)를 비교해보면, DFT는 윈도우된 신호 세그먼트의 DTFT에서 주파수 샘플링한 형태로 나타난다는 걸 알 수 있습니다. 그렇기 때문에, DFT를 사용해서 Fourier analysis를 해석하고자 한다면, 시간 영역에서 windowing과 주파수 영역에서 sampling의 영향에 대해 명확히 이해할 필요가 있습니다.
시간 영역에서 windowing을 어떻게 하느냐에 따라, trade-off 현상이 발생하는데요. 시간 영역의 window를 짧게 잡으면, main lobe에서 주파수 성분의 resolution가 증가하지만 side lobe의 attenuation이 크게 발생하지 않아 원래 주파수 성분이 엉뚱한 곳에 생기는 spectral leakage 현상이 발생하게 됩니다. 반대로, 시간 영역의 window를 길게 잡을 경우, main lobe의 resolution은 상대적으로 감소하고 side lobe의 attenuation이 커집니다.
아래 글은 window 길이가 hamming window와 rectangular window에 미치는 영향을 분석한 글입니다. 참고하시면 좋을 것 같아 첨부하였습니다 :)
Hamming window와 Rectangular window 비교
window 개념을 살펴보기 전에, 왜 신호를 짧은 시간 단위로 나눠 주파수 분석을 수행하는지에 대해 알아봅시다. STFT를 하는 이유 음성 신호는 time-varying, non-stationary 특성을 가지고 있어서 정확한
sunny-archive.tistory.com
주파수 영역에서 sampling을 어떻게 하느냐에 따라, 부정확한 spectrum을 얻게 될 수 있기에 면밀한 신호 분석이 필요합니다. 앞으로 다룰 예제에서 차근차근 살펴보도록 하겠습니다.
Windowing의 영향


시간 영역에서 짧은 윈도우를 적용하면, $\Omega_0$와 $\Omega_1$의 간격도 가까워지게 되는데요. 이 경우, 주파수 영역에서 두 개의 peak가 하나의 peak로 합쳐져 frequency resolution이 줄어드는 문제가 발생합니다.
Spectral sampling의 영향

DFT 샘플링 주기가 길수록 (DFT 주파수 샘플 수가 적을수록), 실제 peak가 DFT 포인트 사이에 있어서 인식하지 못하는 문제가 발생하기도 합니다. 이 문제는 zero padding 또는 window length를 조정하는 것으로 완화할 수 있습니다.
* zero padding
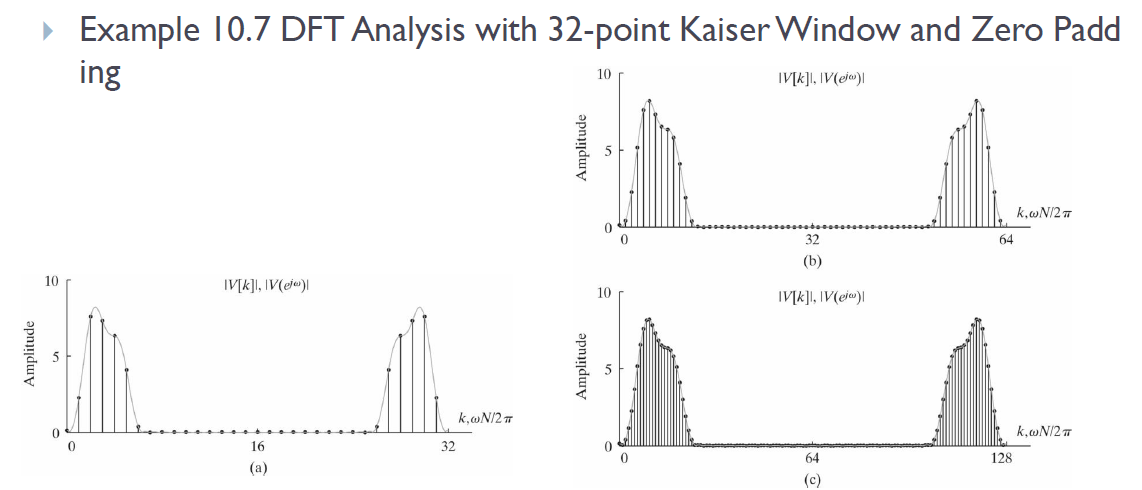
zero padding은 주파수 영역에서 더 많은 샘플을 가지도록 하는 방법입니다. 하지만, 그저 0값만 추가해주는 작업이기 때문에 실제 신호 정보는 변하지 않아 frequency resolution이 개선되지는 않습니다.
* window length
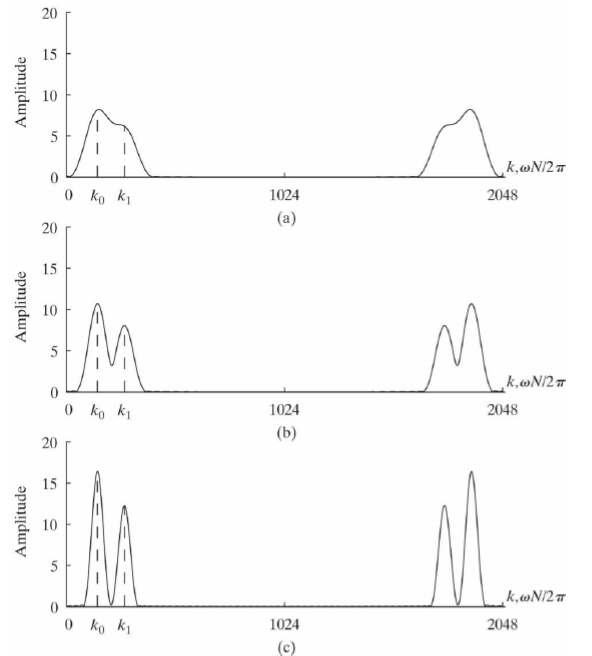
1024 point DFT 상황에서, window length가 32, 42, 64로 길어질 때의 경우를 나타낸 그림입니다. 긴 윈도우를 쓰면, 실제로 쓰는 입력 샘플의 수가 많아지기 때문에 frequency resolution이 더 좋아진다는 것을 확인할 수 있습니다.
Time-Dependent Fourier Transform (STFT)

신호의 통계치가 시간에 따라 변하는 nonstationary 신호의 경우, 전체 신호를 한꺼번에 분석하는 것은 적절하지 않습니다. 이 문제를 해결하기 위해서, 시간에 따른 변화를 반영할 수 있도록 윈도우를 이용해 짧은 세그먼트로 신호를 나눠서 분석하는 STFT를 사용할 수 있습니다.
STFT에 대한 자세한 설명은 아래 글을 참고해주세요 :)
Python으로 STFT 직접 구현해보기
STFT (Short-time Fourier Transform) 정의와 개념 및 필요성을 알아보고 코드로 직접 구현해봅시다. STFT음성 신호는 시간에 따라 변화하고 (time-varying) 신호의 통계적 특성이 지속적으로 변하는 (nonstat
sunny-archive.tistory.com
Spectrogram
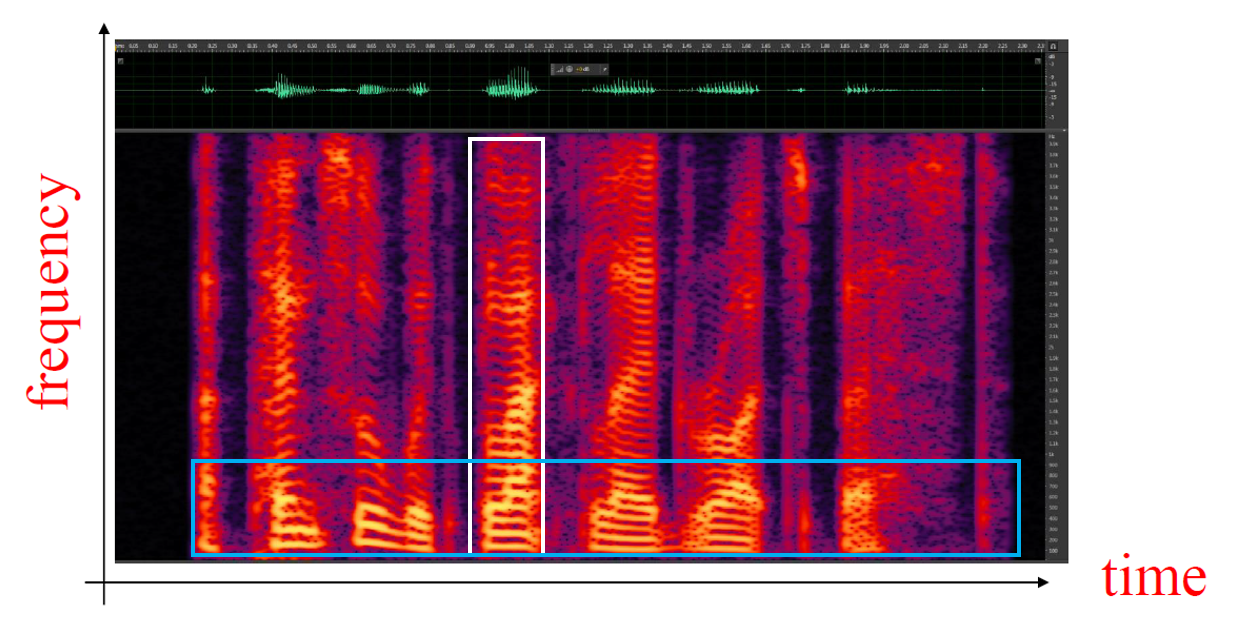
Spectrogram에서 $x$축은 time index, $y$축은 frequency index, color는 신호의 magnitude spectrum을 나타냅니다. 가로로 잘라 보면, 특정 주파수 대역이 시간에 따라 어떻게 변해가는지를 알 수 있습니다. 세로로 잘라 보면, 특정 frame에서의 magnitude spectrum을 관찰할 수 있습니다.
GIST 신종원 교수님 '디지털신호처리' 수업 자료를 바탕으로 쓴 글입니다.
'연구 노트 > 디지털신호처리' 카테고리의 다른 글
| DSP Signal flow 문제 오답 정리 (0) | 2024.06.17 |
|---|---|
| DFT (Discrete Fourier Transform) 바로 알기 (0) | 2024.06.09 |
| 선형 컨볼루션 (Linear convolution)과 원형 컨볼루션 (Circular convolution) (1) | 2024.06.07 |
| DFS (Discrete Fourier Series) 바로 알기 (0) | 2024.06.01 |
| 다운샘플링 시 Aliasing 현상 Spectrogram에서 관찰하기 (0) | 2024.04.21 |



