선형 컨볼루션 (Linear convolution)과 원형 컨볼루션 (Circular convolution)

선형 컨볼루션과 원형 컨볼루션의 개념에 대해 알아보고 파이썬 코드로 구현해 봅시다. 

 

Linear convolution

 

linear convoluton은 주어진 두 개의 이산 시간 신호를 이용하여 새로운 신호를 생성합니다. 식으로 자세히 설명드리자면, 모든 정수 $k$에 대해, 입력 신호 $x[k]$와 시스템 응답 $h[n-k]$의 곱을 합산하는 방식으로 값을 구합니다.

 

 

입력으로 $x[n]$, 시스템 임펄스 응답으로 $h[n]$이 위와 같이 주어졌다고 가정해봅시다. linear convolution은 두 신호가 겹치는 모든 위치에서 합산이 이루어집니다. 따라서, 신호가 완전히 겹치는 모든 부분을 포함하여 결과를 생성합니다.

 

Circular convolution

Circular convolution은 두 신호의 순환적인 특성을 이용한 컨볼루션입니다. DFT와 circular convolution은 밀접한 관계를 가지고 있는데요. 왜 그런지 알아보겠습니다. DFT는 입력 신호를 주기적인 신호로 간주하여 처리합니다. 시간 영역에서 두 신호의 circular convolution은 주파수 영역에서 두 신호의 DFT 곱과 같습니다. 이러한 특성 덕분에, circular convolution을 할 때, DFT와 IDFT를 사용하면 계산 효율성을 높일 수 있습니다.

 

 

circular convolution을 하려면, 먼저, 두 신호 $x[n]$과 $h[n]$의 길이를 $N$으로 맞춰줘야 합니다. 필요한 경우에는, 신호에 zero padding을 적용하여 길이를 맞추고, 각 샘플 $n$에 대해 곱하고 더해줌으로써 circular convolution을 수행할 수 있습니다. (각 $n$에 대해, 모든 $k$에 대한 합을 구해줍니다) 

 

 

입력 신호와 임펄스 응답은 앞의 예시와 동일합니다. $y[0]$을 구하기 위해서, 먼저 $h[n]$을 역순으로 재배치하여 $h^{'}[n]$을 구하고 $x[n]$의 첫번째 원소와 $h[n]$의 첫번째 원소를 묶어둔 후, 나머지 원소들을 순서대로 갖다 붙입니다. 이후, 각 원소들을 곱한 값을 모두 합하면 $y[0]$을 얻을 수 있습니다.

 

 

$y[1]$을 구할 때는, $h^{'}[n]$을 옆으로 밀어서 $x[1]$과 $h[1]$까지의 원소들을 역순으로 묶어두고 나머지 원소들을 순서대로 붙여주면 됩니다.

 

 

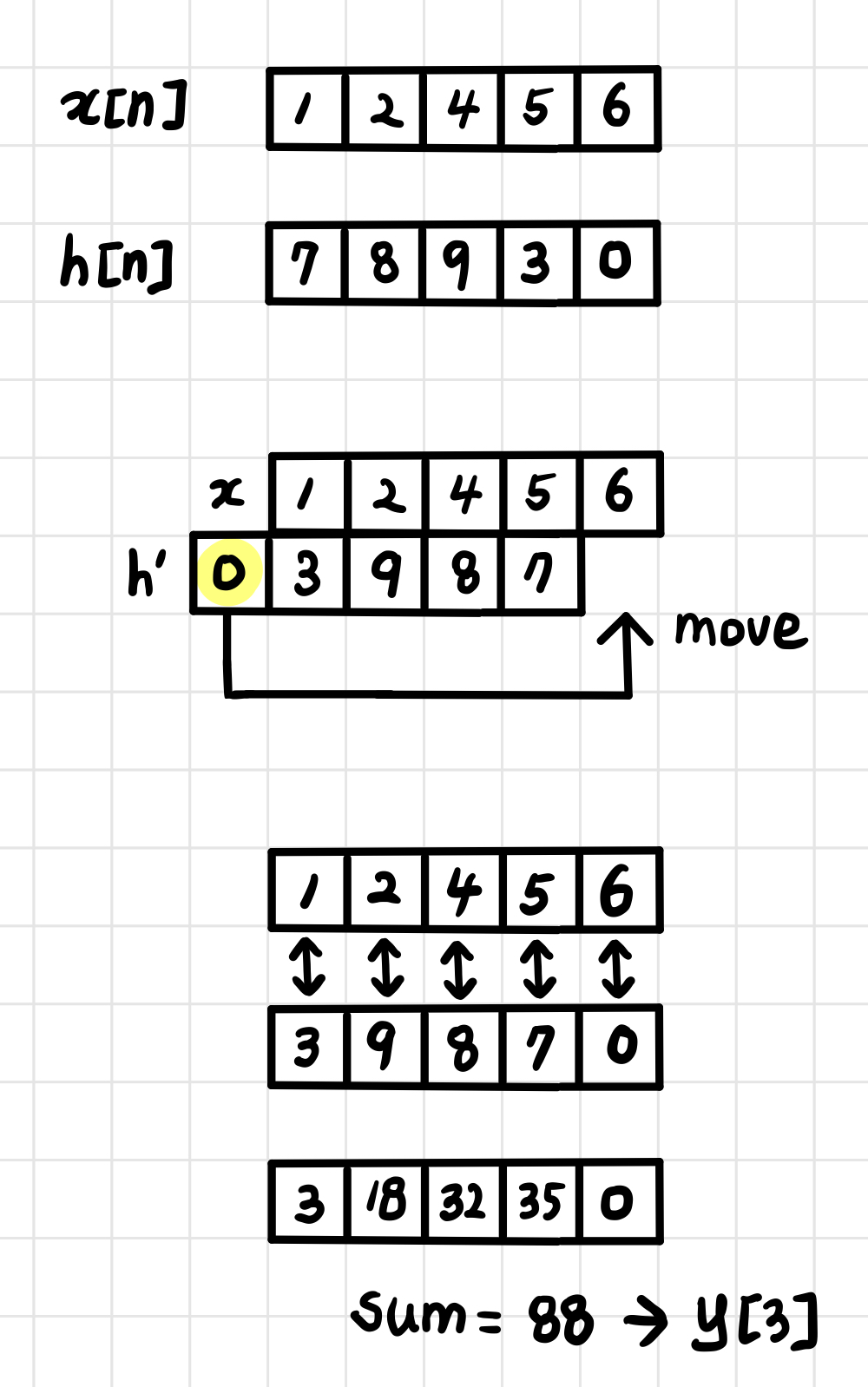
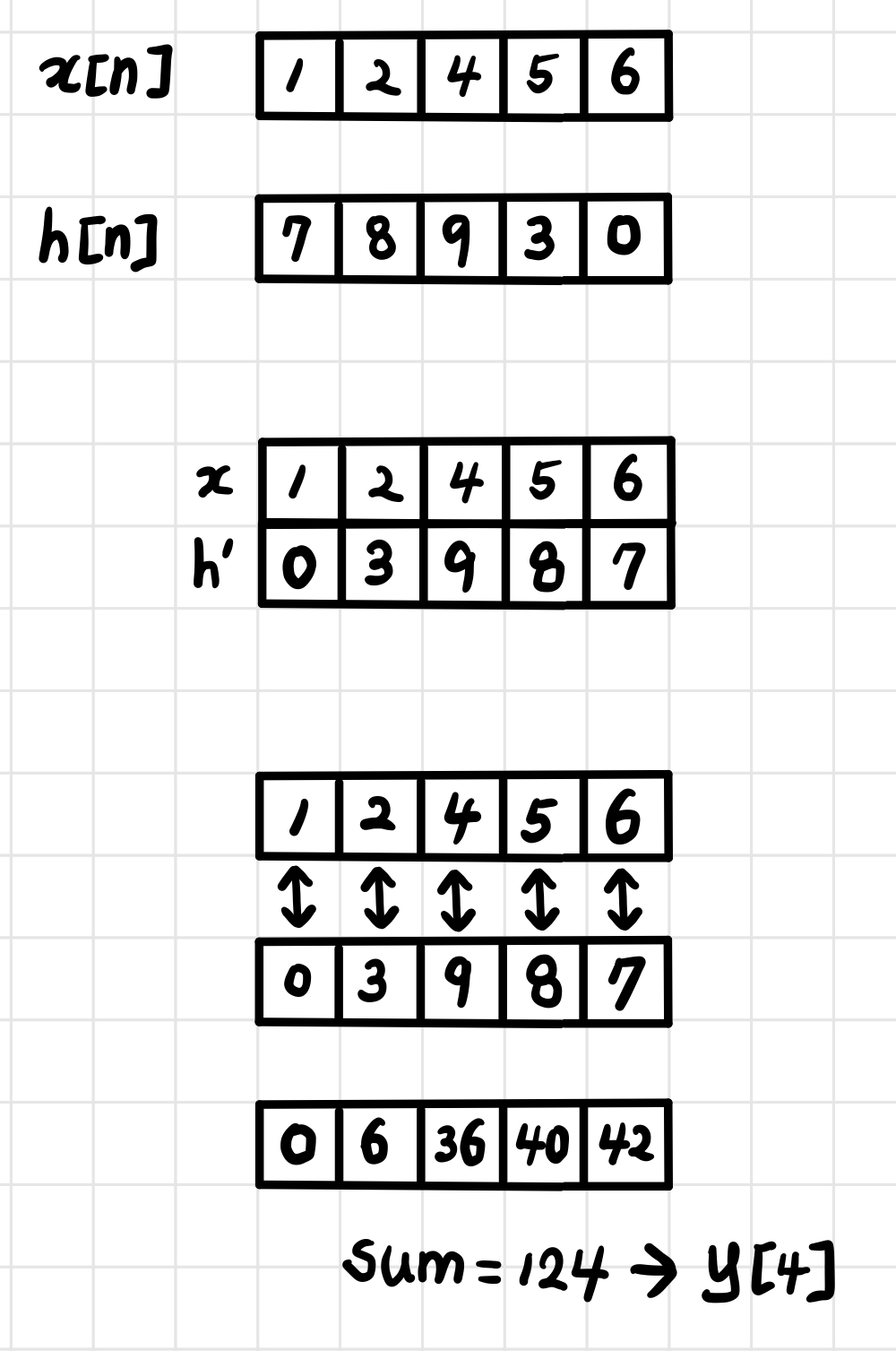
똑같은 방식으로, 마지막 output 원소까지 값을 구할 수 있습니다.

 

Linear convolution / Circular convolution 구현

import numpy as np

x = np.array([1,2,4,5,6])
h = np.array([7,8,9,3,0])

# Linear convolution
def linear_convolution(x,h):
    L = len(x)
    P = len(h)
    y = np.zeros(L+P-1)
    for n in range(L+P-1):
        for k in range(L):
            if 0 <= n-k < P:
                y[n] += x[k] * h[n-k]
    return y
    
# Circular convolution
def circular_convolution(x,h):
    L = len(x)
    y = np.zeros(L)
    for n in range(L):
        for k in range(L):
            y[n] += x[k] * h[(n-k)%L]
    return y


# Linear convolution Result
y_linear = linear_convolution(x,h)
print("Linear convolution:", y_linear)

# Circular convolution Result
y_circular = circular_convolution(x,h)
print("Circular convolution:", y_circular)

## Linear convolution: [  7.  22.  53.  88. 124. 105.  69.  18.   0.]
## Circular convolution: [112.  91.  71.  88. 124.]

 

 $x[n]$의 길이가 $L$이고 $h[n]$의 길이가 $P$라고 했을 때, linear convolution 결과인 $y[n]$의 길이는 $L+P-1$이 됩니다. 반면에, circular convolution은 주기적인 신호라고 가정하기 때문에, 입력 신호의 길이와 같은 $L$이 됩니다. 만약 신호가 충분히 길다면 ($N\geq L+P-1$, $N$은 신호의 한 주기), circular convolution과 linear convolution은 동일한 결과가 나오게 됩니다.

 

FFT 결과 확인

import torch
import torch.fft

x = torch.Tensor([1,2,4,5,6])
h = torch.Tensor([7,8,9,3,0])

X = torch.fft.fft(x)
H = torch.fft.fft(h)
y = torch.fft.ifft(X*H).real

print("y[n] =", y.numpy().round())
## y[n] = [112.  91.  71.  88. 124.]

 

FFT는 DFT를 빠르게 계산하는 알고리즘입니다. $x[n]$과 $h[n]$이 위 예시와 똑같이 주어졌을 때, 각 신호의 FFT 곱을 다시 inverse FFT한 결과는 시간 영역에서 circular convolution 결과와 같다는 걸 코드를 통해 확인할 수 있습니다.

 

• FFT 시간 복잡도: $O(N \log N)$
• DFT 시간 복잡도: $O(N^2)$