이산 푸리에 급수 (DFS)의 정의와 특성을 알아보고 예시를 통해 개념을 정리해봅시다.
DFS (Discrete Fourier Series)

DFS는 주기성을 갖는 discrete signal을 주파수 성분들의 합으로 표현하는 방법입니다. 이때, 각각의 주파수 성분은 특정 주파수에 해당하는 기저 함수 (basis function)로 표현할 수 있습니다. 위 신호에서 fundamental period는 $N$이고 fundamental frequency는 $\omega_0=2\pi / N$으로 표기합니다.

주파수 성분들은 fundamental frequency $\frac{2\pi}{N}$의 정수 배로 주어지기 때문에, DFS는 periodic signal을 조화적 관계를 갖는 (harmonically related) 복소 지수 함수 (complex exponential)의 선형 결합으로 나타낼 수 있습니다. 이는 주기성을 갖는 discrete signal을 다양한 주파수 성분으로 분해할 수 있다는 걸 의미합니다.

순서대로 DFS analysis, synthesis를 나타낸 식입니다.여기서 $\tilde{X}[k]$는 주파수 $\frac{2\pi k}{N}$에 해당하는, $x[n]$의 k번째 주파수 성분으로 DFS 계수입니다. $e^{j\frac{2\pi}{N}kn}$은 특정 주파수를 나타내는 복소 지수 함수이고 $k$는 $0$부터 $N-1$까지의 정수입니다.



정리해보자면, DFS는 periodic discrete signal을 harmonically related complex exponential의 선형 결합으로 표현할 수 있습니다. 이 과정을 통해, 신호를 여러 개의 주파수 성분으로 분해하여 각 성분의 기여도를 파악할 수 있게 됩니다. 각각의 주파수 성분은 fundamental frequency의 정수 배로, 한 주기 동안의 값들을 모두 합하면 원래의 periodic signal을 재구성 할 수 있습니다.
DFS 예시 살펴보기
* Periodic Imuplse Train의 DFS

* DFS의 duality

* Periodic Rectangular Pulse Train의 DFS

0~4까지는 1 값을 갖고 5~9까지 0 값을 갖는 주기가 $N=10$ 인 periodic sequence의 DFS 식은 위와 같이 등비급수 공식을 통해 계산됩니다. 오른쪽 그래프를 살펴보면, DFS 계수의 magnitude는 싱크 함수 형태로 그려지고 0값을 가질 때 phase가 정의되지 않는 걸 확인할 수 있습니다.
DFS의 Property
* Linearity
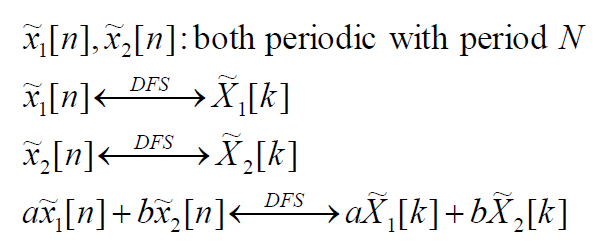
* Shift of a sequence
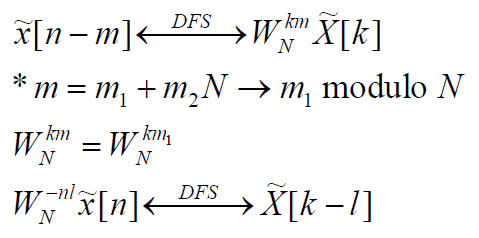
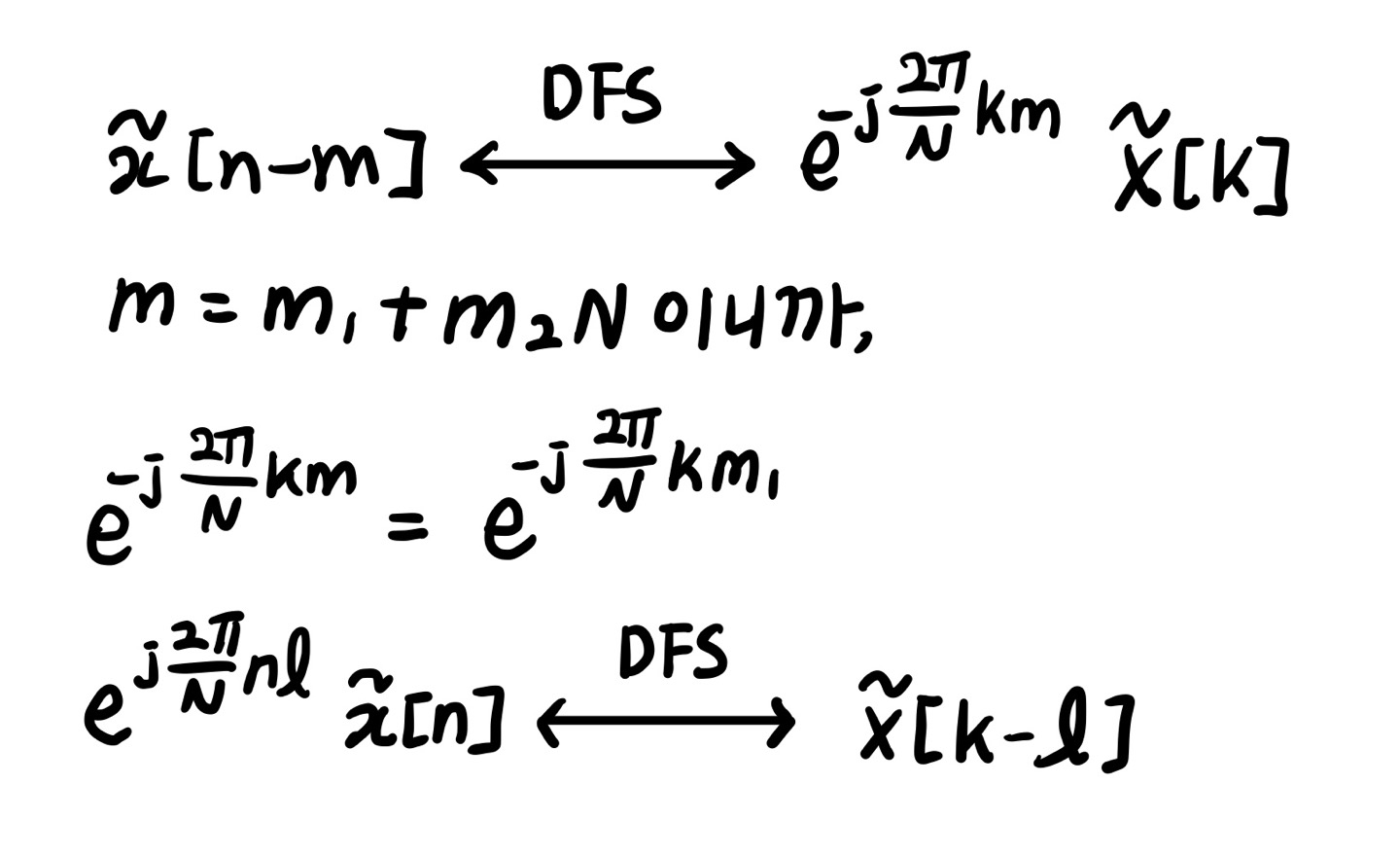
* Duality
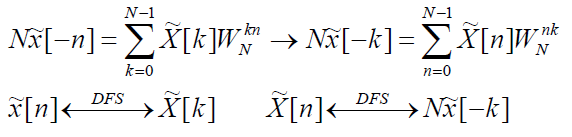
* Periodic Convolution
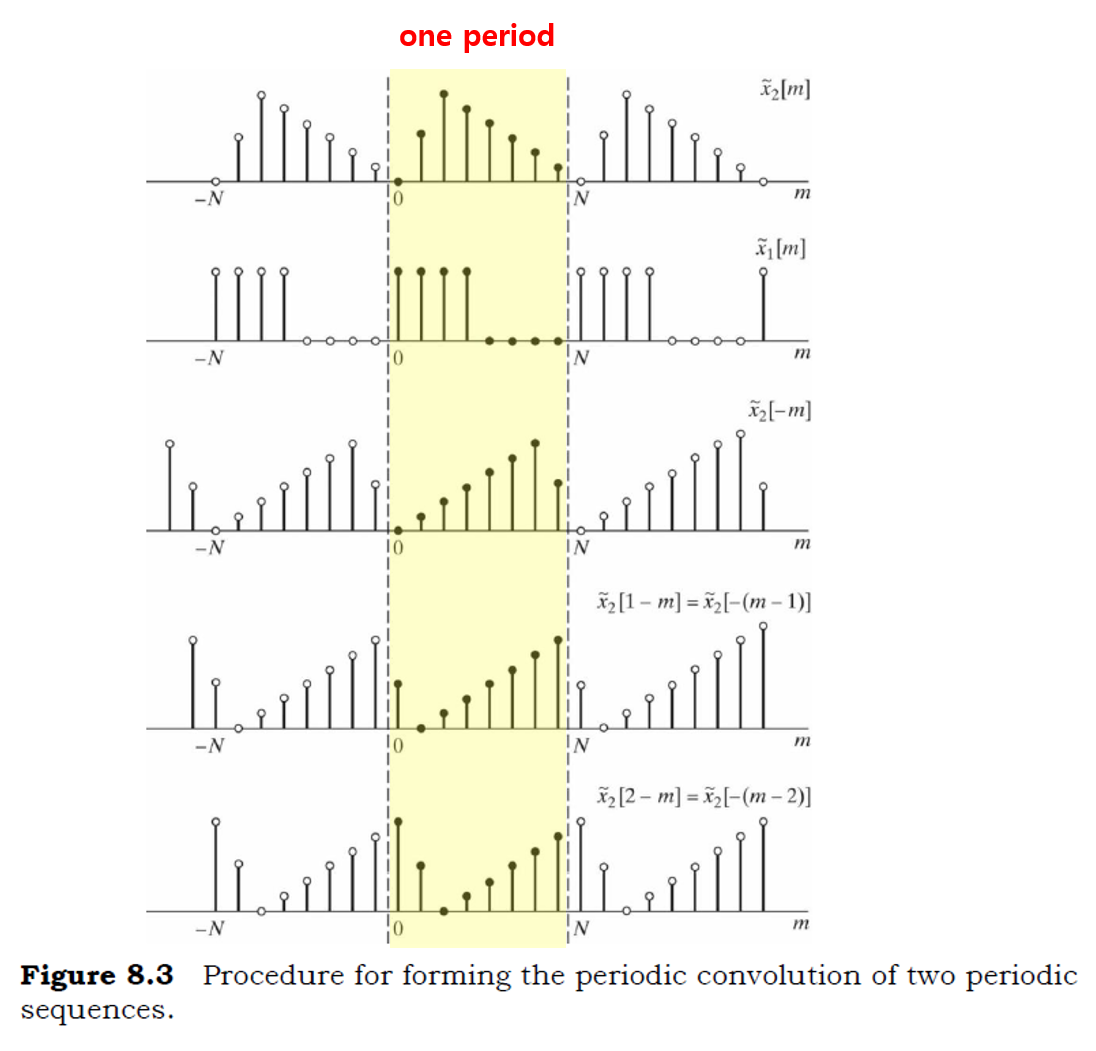
Periodic convolution은 주기적으로 반복되는 신호에 대한 컨볼루션을 수행합니다. 주기성을 갖는 시퀀스는 한 주기 간격으로 각 자리의 값을 곱하고 더하기를 반복합니다.
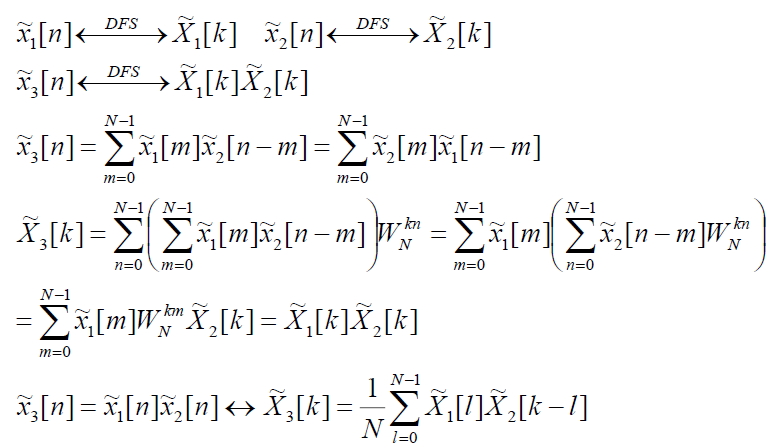
일반적인 linear convolution과는 달리, periodic convolution은 인덱스가 modulo $N$ 연산을 통해 순환됩니다. 즉, 샘플 $n$마다 주기적으로 반복됩니다.
Property 한 눈에 보기


GIST 신종원 교수님 '디지털신호처리' 수업 자료를 바탕으로 쓴 글입니다.
'연구 노트 > 디지털신호처리' 카테고리의 다른 글
| DFT (Discrete Fourier Transform) 바로 알기 (0) | 2024.06.09 |
|---|---|
| 선형 컨볼루션 (Linear convolution)과 원형 컨볼루션 (Circular convolution) (1) | 2024.06.07 |
| 다운샘플링 시 Aliasing 현상 Spectrogram에서 관찰하기 (0) | 2024.04.21 |
| 고윳값 (eigenvalue), 고유 함수 (eigenfunction) 개념으로 LTI 시스템 해석하기 (0) | 2024.04.18 |
| LTI 시스템의 주파수 응답과 phase distortion, group delay (1) | 2024.04.13 |



