MVDR beamformer 유도 (Feat. 라그랑주 승수법)

Narrowband라고 가정했을 때, MVDR beamformer를 라그랑주 승수법 (Lagrange Multiplier Method)을 이용해 직접 풀어봅시다. 
 
* Note! (소문자: scalar, 볼드체 소문자: vector)로 표기하였습니다. / 필기본에서는 notation이 다소 정확하지 않을 수 있으니 본문을 참고해주시기 바랍니다.
 

Narrowband model Criterion 

 
Narrowband model을 가정하는 이유는 노란색으로 표시된 식과 같이 frequency 별로 independent한 식을 쓰기 위함 입니다. 식은, '소스 신호를 STFT한 $s_j(n,f)$와 소스 신호의 여러 개의 전파 경로를 합산한 결과를 STFT한 $\textbf{a}_j(n,f)$를 곱한 것은 마이크에 녹음된 소리에 대한 소스의 기여도를 나타낸 spatial image $\textbf{c}_j(n,f)$와 같다'로 해석할 수 있겠습니다. Narrowband model은 위에 나온 몇 가지 가정을 바탕으로 criterion이 설계됩니다. 
 

 
MWF (multichannel wiener filter)에 기반을 둔 MVDR beamformer는 MMSE (minimum mean squared error) criterion에 따라 최적화됩니다. 다시 말해, 타겟값과 추정치를 빼서 제곱한 값이 최소화되는 가중치를 구하게끔 설계됩니다. cost function을 풀어보면 speech distortion 항과 noise 항으로 나오는 걸 볼 수 있습니다.

 

 

speech distortion 항을 0으로 설정하면 '신호에 왜곡이 발생하지 않는다'는 constraint 조건 식을 얻을 수 있게 됩니다.
 

MVDR beamformer 

 
먼저 우리가 풀고자 하는 Criterion 식을 살펴보겠습니다. array look direction의 gain을 1이라고, distortionless 제약조건을 설정했습니다. 왜 이런 제약조건이 있을까요? 
 
제약조건이 있어야 beamformer를 써먹을 수 있기 때문입니다. 제약조건이 없다는 가정 하에 weight가 0일 때를 생각해봅시다. noise는 최소화 되겠지만 beamforming을 하는 목적인 desired signal을 구할 수가 없겠죠..
 
따라서, 신호가 왜곡되지 않는다는 제약조건 하에 desired signal을 구해야 합니다. 이 값을 구하기 위해, 라그랑주 승수법을 이용해 MVDR beamformer 최적화 문제를 풀어볼 것입니다. 최적화하려는 값에 dummy variable인 $\lambda$, 라그랑주 승수 (Lagrange multiplier) 항을 추가함으로써, 제약된 문제를 제약 없는 문제로 바꿔줄 수 있습니다.
 

MVDR beamformer 유도

 
싱글 소스라고 가정했을 때, 마이크 신호를 $\mathbf{x}$를 다음과 같이 source에서 마이크로 전달되는 신호 $( \mathbf{a}_1 s_1)$와 noise 신호 $( \mathbf{u})$를 더한 식으로 정의해봅시다. 여기서 우리가 원하는 신호는 $s_1$ 입니다. 

 
원하는 신호 $(s_1)$가 deterministic 하다고 가정해봅시다. Beamformer 출력값은 가중치 벡터 $(\mathbf{w}^H)$와 마이크 신호 $(\mathbf{x})$를 곱한 값으로 정의됩니다. 이를 다시 source와 noise 신호의 합 $ ( \mathbf{a}_1 s_1+ \mathbf{u}) $으로 바꿔 적어줍니다. 신호가 왜곡되지 않으면서 최적화 조건을 달성한 weight 값을 원하기 때문에 gain을 1로 설정해줍니다. weight 벡터에 noise signal을 곱한 항에서 도출된 $E \left\{ \mathbf{u} \mathbf{u}^H \right\}$은 noise spatial covariance matrix (noise SCM)가 됩니다. 
 
* deterministic: 한 입력이 들어오면 언제나 똑같은 과정을 거쳐 예상한 결과가 나오는 예측 가능한 성질을 말함

 

 

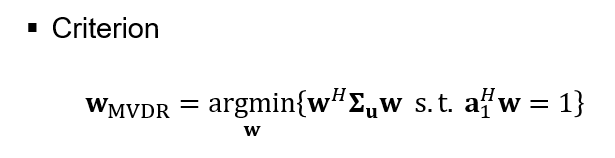
이제 라그랑주 승수법을 이용하여,  distortionless를 만족한다는 제약조건 하에 noise variance를 최소화하는 가중치 벡터를 찾는 최적화 문제를 풀어보겠습니다.

 

 

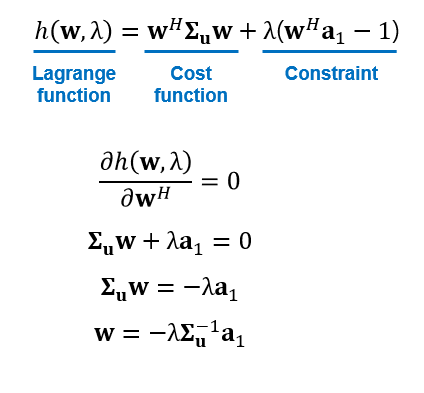
먼저 라그랑주 함수 $h(\mathbf{w}, \lambda)$를 정의해주었습니다. cost function과 constraint가 하나의 식으로 합쳐진 걸 알 수 있습니다. 라그랑주 함수 $h(\mathbf{w}, \lambda)$에서 $\mathbf{w}^H$에 대해 미분한 값이 0이라고 설정함으로써, gain을 나타내는 스칼라 값인 라그랑주 승수와 direction을 나타내는 noise variance에 대한 식으로 $\mathbf{w}$를 정의할 수 있게 됩니다.

 

  
constraint 식을 이용하면 라그랑주 승수 값을 구해줄 수 있는데 이 값을 앞에서 구한 $\mathbf{w}$ 식에 대입해주면 우리가 원하는 솔루션이 나옵니다! ㅠㅠ
 

Reference

[1] S. Gannot, E. Vincent, S. Markovich-Golan, and A. Ozerov, “A Consolidated Perspective on Multimicrophone Speech Enhancement and Source Separation,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 25, no. 4, pp. 692–730, Apr. 2017, doi: https://doi.org/10.1109/taslp.2016.2647702.
[‌2] C. Hogstrom, “Adaptive Beamforming Tutorial Part 2: Preserving the Signal of Interest - Gritty Engineer,” Jan. 11, 2020. https://grittyengineer.com/adaptive-beamforming-tutorial-part-2-preserving-the-signal-of-interest/ (accessed Mar. 15, 2024).
[3] “Matrix calculus,” Wikipedia, Feb. 05, 2024. https://en.m.wikipedia.org/wiki/Matrix_calculus (accessed Mar. 16, 2024).

‌