STFT (Short-time Fourier Transform) 정의와 개념 및 필요성을 알아보고 코드로 직접 구현해봅시다.
STFT
음성 신호는 시간에 따라 변화하고 (time-varying) 신호의 통계적 특성이 지속적으로 변하는 (nonstationary) 성질을 가지고 있기 때문에 전체 신호를 가지고 분석하는데 어려움이 있습니다. 하지만, 음성 신호를 아주 짧은 부분으로로 나누어 보면 각 세그먼트가 일정한 주기로 패턴이 반복되는 걸 관찰할 수 있습니다. 이러한 이유로, 음성 신호 처리에서는 윈도우 (window)를 사용하여 신호를 짧은 세그먼트로 나눈 후 각 세그먼트에 대해 DFT (discrete fourier transform)를 수행하는 STFT (short-time fourier transform)를 사용합니다. STFT를 통해, 각 세그먼트의 주파수 영역 상 특징 (feature)을 추출함으로써 음성 신호의 주파수 성분이 시간에 따라 어떻게 변하는지 파악할 수 있으므로 신호를 더 효과적으로 분석 및 처리할 수 있습니다.



식을 보면, 원신호
아래 글은 참고하시면 좋을 것 같아 첨부하였습니다 :)
FFT 수행 시 zero padding이 frequency resolution에 미치는 영향
STFT 결과로 얻게 된 frequency bin이 무엇인지 알아보고 FFT 수행 과정에서 zero padding이 frequency resolution에 어떤 영향을 미치는지 알아봅시다. STFT (Short-time Fourier Transform) 자연적으로 발화되는 음성은
sunny-archive.tistory.com
STFT 결과
STFT의 결과는 복소수 행렬 (complex-valued matrix)로 표현됩니다. 행은 주파수 성분을 나타내고, 열은 시간 프레임을 나타냅니다. 이 행렬의 요소들은 각 시간-주파수 (time-frequency) 블록에서 주파수 성분의 크기와 위상을 나타냅니다. 복소수의 크기 (magnitude)는 해당 시간 프레임에서의 주파수 성분의 강도를 나타내고, 복소수의 위상 (phase or angle)은 해당 주파수 성분의 위상을 나타냅니다.
STFT 파이썬 라이브러리 구현
순서대로 librosa, torchaudio 라이브러리로 STFT를 수행하여 spectrogram을 출력한 코드입니다.
## librosa 라이브러리 이용 ##
import numpy as np
import librosa
import librosa.display
import matplotlib.pyplot as plt
waveform, sample_rate = librosa.load('Original.wav')
x = waveform
y = librosa.stft(x, n_fft=512, hop_length=128, win_length=512, window='hamming')
magnitude = np.abs(y)
log_spectrogram = librosa.amplitude_to_db(magnitude)
plt.figure(figsize=(10,4))
librosa.display.specshow(log_spectrogram, sr=16000, hop_length=128)
plt.xlabel("Time")
plt.ylabel("Frequency")
plt.colorbar(format='%+2.0f dB')
plt.title("Spectrogram (dB)")

## torchaudio 라이브러리 이용 ##
# 입력 신호 로드
waveform, sample_rate = torchaudio.load('Original.wav')
# STFT 파라미터 설정
window_size = 512
hop_size = 128
n_mels = 128
# STFT 변환기 생성
stft_transform = transforms.Spectrogram(n_fft=window_size, \
hop_length=hop_size, window_fn=torch.hamming_window)
# STFT 계산
stft = stft_transform(waveform)
# Mel 스펙트로그램 변환기 생성
mel_spec_transform = transforms.MelSpectrogram(sample_rate=sample_rate, \
n_fft=window_size, hop_length=hop_size, \
n_mels=n_mels)
# Mel 스펙트로그램 계산
mel_spec = mel_spec_transform(waveform)
# 결과 시각화: 일반적인 STFT magnitude
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.imshow(torch.log(torch.abs(stft) + 1e-9).squeeze().numpy(), \
aspect='auto', origin='lower')
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.title('Spectrogram')
plt.colorbar(format='%+2.0f dB')
# 결과 시각화: Mel 스케일로 변환한 STFT magnitude
plt.subplot(1, 2, 2)
plt.imshow(torch.log(mel_spec + 1e-9).squeeze().numpy(), \
aspect='auto', origin='lower')
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.title('Mel Spectrogram')
plt.colorbar(format='%+2.0f dB')
plt.tight_layout()
plt.show()

STFT 직접 구현
위 이론 식을 바탕으로, STFT 함수를 구현하여 spectrogram을 출력한 코드입니다.
# 신호, 윈도우 길이, 프레임 shift를 인자로 받음
def stft_func(x, window_length, hop_size):
# 해밍 윈도우 생성
window = np.hamming(window_length)
# 프레임 개수 계산
frame_num = 1 + int((len(x) - window_length) / hop_size)
# STFT 결과 저장 배열
stft_spectrogram = np.zeros((frame_num, window_length // 2 + 1), \
dtype=complex)
# STFT 수행
for frame_idx in range(frame_num):
# 프레임의 시작/끝 인덱스
start_idx = frame_idx * hop_size
end_idx = start_idx + window_length
# 프레임 신호 추출
framed_signal = window * x[start_idx:end_idx]
# DFT 계산 (frequency bins / time frames)
time_idx = np.expand_dims(np.arange(window_length), 0)
freq_idx = np.expand_dims(np.arange(window_length // 2 + 1), 1)
dft_exp = np.exp(-1j * 2 * np.pi * freq_idx * time_idx / window_length)
stft_spectrogram[frame_idx] = (np.expand_dims(framed_signal, 0) \
* dft_exp).sum(1)
return stft_spectrogram
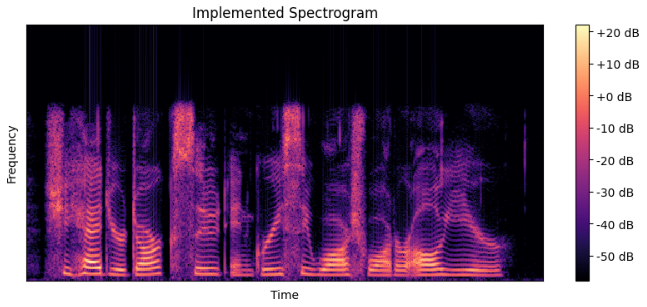
librosa 라이브러리를 사용한 결과와 거의 동일하게 나온 걸 확인할 수 있습니다 :)
'연구 노트 > 음성신호처리' 카테고리의 다른 글
| 2024.05.30 신입생 세미나 The Cepstrum and Homomorphic Speech Processing 질문 정리 1/2 (0) | 2024.05.30 |
|---|---|
| 2024.05.23 신입생 세미나 Frequency-Domain Representations 질문 정리 (0) | 2024.05.23 |
| 2024.05.16 신입생 세미나 Frequency-Domain Representations 질문 정리 (0) | 2024.05.16 |
| 2024.05.09 신입생 세미나 Frequency-Domain Representations 질문 정리 (0) | 2024.05.09 |
| Coherence 개념으로 Diffuse noise 모델링 (0) | 2024.05.09 |



