FFT 수행 시 zero padding이 frequency resolution에 미치는 영향

STFT 결과로 얻게 된 frequency bin이 무엇인지 알아보고 FFT 수행 과정에서 zero padding이 frequency resolution에 어떤 영향을 미치는지 알아봅시다.

 

STFT (Short-time Fourier Transform)

자연적으로 발화되는 음성은 시간에 따라 계속해서 변하는 성질을 가지고 있기 때문에, 음성 신호를 표현하는데 있어 일반적인 Fourier 표현 방법을 적용하는 건 한계가 있습니다. 이 문제를 해결하기 위해, 음성 신호를 주파수 영역에서 분석할 수 있도록, STFT, 즉, 음성 신호를 짧은 세그먼트 단위로 나눠 DFT를 수행하게 됩니다. 

 

Frequency bin

STFT 결과는 frequency, time 값들로 이루어진 2차원 행렬로서 표현이 가능한데 이때 특정 time에서 갖는 frequency 값을 frequency bin이라고 합니다.

 

STFT 결과

 

STFT에 대한 구체적인 내용 또는 직접 구현한 코드를 살펴보고 싶다면 아래 링크를 참고해주세요 :)

 

STFT (Short-time Fourier Transform) 코드 직접 구현해보기

 

Frequency resolution

인접한 여러 개의 주파수 중 서로 다른 주파수 성분을 구별할 수 있는지를 나타낸 게 바로 분해능 (frequency resolution) 입니다. 원하는 신호를 frequency domain에서 관찰할 때 얼마나 촘촘한 간격으로 해당 주파수 성분 값을 관찰할 수 있는지를 나타냅니다.

 

---

512 point로 DFT 했을 때, frequency bin이 몇 개 나올까요?

 

시퀀스의 길이가 N일 때 DTFT, DFT 식을 살펴보겠습니다. DFT식의 $N$은 sampling frequency를 몇 point로 나눌 것인지를 의미하고 $k$는 몇 번째 frequency bin인지를 나타냅니다. $k$값의 범위가 $0$부터 $N-1$까지 이기 때문에 'frequency bin은 N개가 아닐까?'라고 생각할 수 있겠지만 나이퀴스트 샘플링 이론에 따라 $\pi$를 넘어가는 주파수에 대해서는 앨리어싱이 발생하기 때문에 (주파수 성분이 $\pi$ 이하일 때와 똑같이 나옴), frequency bin의 개수는 $(\frac{N}{2}+1)$개가 나오게 됩니다. 따라서, 512 point로 DFT 했을 때의 frequency bin의 수는 257개가 되겠습니다!~

 

Sampling rate가 16kHz일 때, 1024 point로 FFT 하면 한 frequency bin은 몇 Hz일까요?

0~16kHz에 1024개의 data point가 있다는 것은 곧, 전체 16kHz 범위를 1024개 간격으로 나눴다는 것을 의미합니다. 추가로, 당연한 말이지만 FFT size가 늘어나게 되면 data point도 늘어나는 것이기 때문에 연산량이 증가합니다.

 

Frequency resolution $ = \frac{Sampling\,rate}{FFT\,point} = \frac{16000}{1024} \approx 15.625$ Hz/bin

 

frequency resolution은 위 공식처럼 sampling rate를 FFT point로 나눈 값으로 정의할 수 있습니다. 위 공식에서 알 수 있듯이, frequency resolution은 한 개의 frequency bin이 나타내는 주파수 대역을 의미합니다. 따라서, 한 frequency bin은 약 15.625Hz 입니다.

 

 

다음은 Hamming window를 사용하여 long window(narrowband), short window(wideband)일 때의 voiced speech의 waveform(a)과 spectrum(b)을 나타낸 그림입니다. wideband보다 narrowband에서 frequency bin 간격이 더 좁은 것을 확인할 수 있습니다. frequency bin 간격이 좁을수록 각각의 주파수 성분들을 더 잘 구별해낼 수 있기 때문에 freqeuncy resolution이 향상됩니다. 

 

512 point FFT를 zero-padding하여 1024 point FFT로 만들어줬을 때, frequency resolution이 향상될까요?

512개의 data point를 가지는 신호가 있다고 가정해봅시다. zero-padding 작업을 통해 이 신호를 1024개의 data point를 가지는 신호로 만들어주었습니다. time domain에서의 신호를 frequency domain에서 관찰하였을 때, resolution은 어떻게 달라질까요? 0값으로 채워넣었으니 아무런 변화가 없을까요? 아니면.. 그래도 데이터 개수가 증가는 했으니 resolution이 향상되었을까요?

 

 

정답부터 얘기하자면, time domain에서 512에서 1024개로 data point를 늘렸을 때 frequency domain에서 resolution은 향상되지 않습니다.

 

 

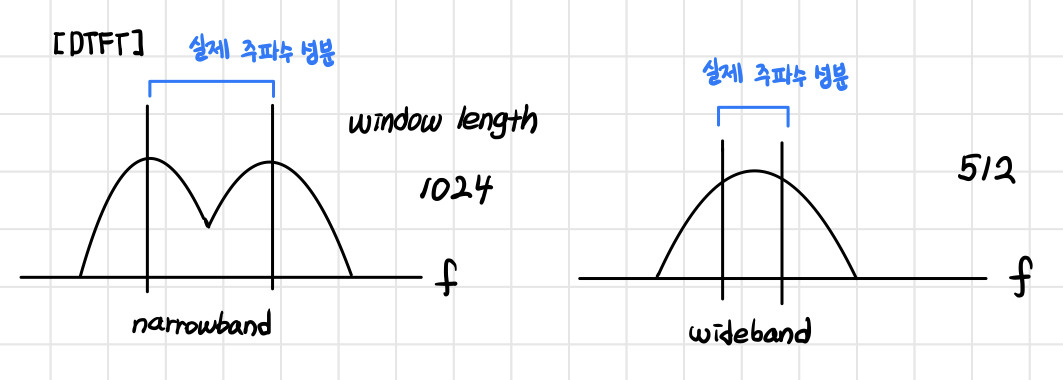
이론상으로 윈도우의 길이가 각각 512, 1024일 때 DTFT한 결과는 다음과 같이 나타납니다. 1024 point의 narrowband에서는 서로 다른 두 개의 주파수 성분을 잘 구분하고 있는 것을 확인할 수 있습니다. 반대로 512 point wideband에서는 두 개의 주파수 성분을 따로 구별하고 있지 않아 frequency resolution이 상대적으로 떨어진다는 것을 알 수 있습니다. 

 

 

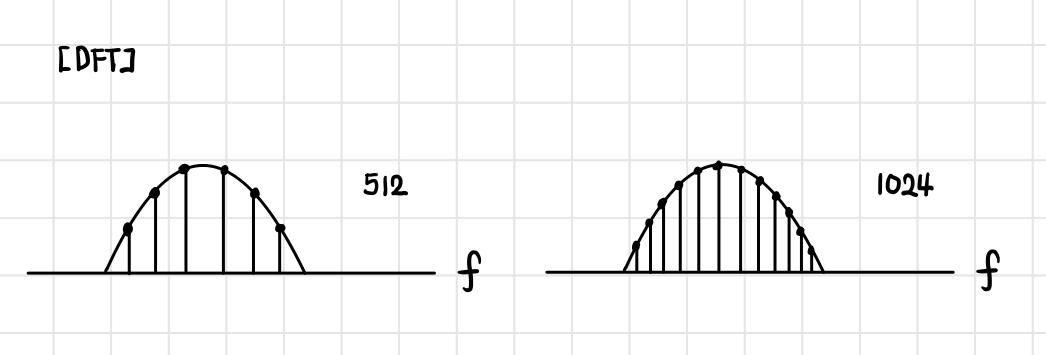
다음은 위에서 보았던 wideband의 경우를 sampling한 DFT 결과를 나타낸 그림입니다. 실제 값이 아닌 단순히 샘플의 개수(data point 개수)가 증가한 것이기 때문에 512 point나 1024 point나 frequency resolution는 크게 달라지지 않습니다.